Maximum Likelihood Estimation in EViews

This post is all about estimating regression models by the method of Maximum Likelihood, using EViews. It's based on a lab. class from one of my grad. econometrics courses.

We don't go through all of the material below in class - PART 3 is left as an exercise for the students to pursue in their own time.

The data and the EViews workfile can be found on the data page and the code page for this blog.

The purpose of this lab. exercise is to help the students to learn how to use EViews to estimate the parameters of a regression model by Maximum Likelihood, when the model is of some non-standard type. Specifically, find lout how to estimate models of types that are not “built in” as a standard option in EViews. This involves setting up the log-likelihood function for the model, based on the assumption of independent observations; and then maximizing this function numerically with respect to the unknown parameters. 

First, to introduce the concepts and commands that are involved, we consider the standard  linear multiple regression model with normal errors, for which we know that the MLE of the coefficient vector is just the same as the OLS estimator. This will give us a “bench-mark” against which to check our understanding of what is going on. Then we can move on to some more general models.

PART 1

Suppose that we have a linear multiple regression model, satisfying all of the usual
assumptions:

where the regressors are non-random. The MLE for the coefficient vector is

and the MLE for the variance of the error term is

Now, we can open the EViews workfile, and estimate a linear regression model, with Y as the dependent variable, and an intercept and X as the two regressors:

So, our simple regression model is:

and the marginal data density for the i^th observation is:

Given the assumed independence of the data, to get the joint data density, and hence the likelihood function, we need to multiply each of the n marginal data densities together:

So, to get the log-likelihood function, we need to add the logarithms of the marginal data densities:

We can see that a typical term that will appear in the expression for the log-likelihood function is of the form:

To get EViews to perform MLE, we have to supply a typical term of the form (3). This is done via the so-called “LOGL” object. In your workfile, click on the "Object" button, and choose the “New Object” option. Then, highlight "LogL" as, shown below. You can supply a name for this object, either now, or later on when you save it – it may be a good idea to call this new object LOGL01 at this stage. 

When you click "OK", this is what you see next:

You can now enter the information for the i^th term in the log-likelihood function:

@logl LL1
eps = y - c(1) - c(2)*x
LL1 = -log(c(3)) - (eps^2)/(2*c(3)^2) - 0.5*log(2*3.14159)

The first line of code declares that we are constructing a log-likelihood function, and are going to call it LL1. (You can use any name you like.) The second line of code is introduced merely to make the expression in the third line a little simpler. Note that we are supplying the expression for just a single log-density. EViews will assume that the data are independent, and do the summing that we see in equation (2) above for us. Here, the coefficients c(1), c(2) and c(3) correspond to β₁, β₂, and σ respectively.

The object box will now look like this:

Next, press the "Estimate" button, and this is what you'll see:

Notice that you have a choice of algorithms for maximizing the Log-Likelihood Function. In evaluating the derivatives you should always choose “accuracy” over “speed”. The following results then emerge when you click “OK”:

The OLS results you saved as EQ01 were as follows:

Why is the estimate of c(3) in the MLE output different from the “standard error of regression” in the OLS output? Why are the standard errors different? You should be able to verify that everything has actually been calculated correctly.

Notice that the “Log likelihood” values are the same in each output – this is the value of the Log-Likelihood Function when the MLE’s for the parameters are substituted into equation for the Log-Likelihood given earlier. It is the maximized value of the Log-Likelihood Function. 

We need to check that the Log-Likelihood Function has been properly maximized. In the LOGL01 output box, click on “View”, “Gradients”, then “Summary”, to get:

The gradients in each direction of the parameter space are evaluated at each point in the sample. These values are summarized by taking the mean and sum of each gradient across the sample values. We see that the gradients are essentially zero, as they should be.

Note:

• In practice, you may need to edit the elements of the coefficient vector before you estimate a model by MLE to make sure that you don’t silly starting values for the maximization algorithm. For example, in this exercise, if we had not already altered the coefficient values by running the initial OLS regression, we would have had to make sure that c(3) did not start of with the (default) value of zero – can you see why?
• If you need to modify the code for the Log-Likelihood specification in the LOGL01 object box, just select “View”, then “Likelihood Specification” in that box’s header bar, and then edit accordingly.

Now we're ready to estimate a non-standard model by MLE.

PART 2

Suppose that instead of assuming Normally distributed errors, you want to allow for “fat tails” (i.e., a higher probability of outliers) in the error distribution. Recall that the Student-t distribution has a density function with this property if the associated degrees of freedom are relatively small. The need to allow for fatter tails in the density may arise, for example, when modelling financial returns. The Student-t distribution has a finite first moment only if ν > 1, where ν is the degrees of freedom parameter. It has a finite second moment only if ν > 2, so probably the smallest value for the degrees of freedom that we should consider is ν = 3.

You probably know that if the errors of our standard multiple linear regression model follow a multivariate Student-t distribution, then the MLE for the coefficient vector is just the OLS estimator. However, this result does not arise if the individual errors are independent Student-t distributed! This is the specification that we'll follow next.  &

To set up the Log-Likelihood function we need to know the formula for the density function for a random variable that is Student-t distributed, with ν degrees of freedom. For a typical value of the error term, this (marginal) density takes the form:

where ‘h’ is a scale parameter and ‘const’ is the normalizing constant that ensures that the density is “proper” – that is, that it integrates to unity. (In the case of the normal density, this is the role that the (2π)^-1/2 term plays.) For the Student-t density, this normalizing constant is:

where the "Gamma function" is defined as

In EViews, we can compute Gamma(x) using the @gamma(x) function.

Using these results, we can again construct the Log-Likelihood function by adding up the logarithms of the marginal data densities:

So, we create a new object and name it (say, LOGL02). Then we use the following code to set up the Log-Likelihood Function for our simple regression model with independent Student-t errors: 

@logl LL2 

eps = y-c(1)-c(2)*x 

v=3 

const=@gamma((v+1)/2)/(@sqrt(v*3.14159)*@gamma(v/2)) 

LL2 = log(const)+0.5*log(c(3))-((v+1)/2)*log(1+c(3)*(eps^2/v)) 

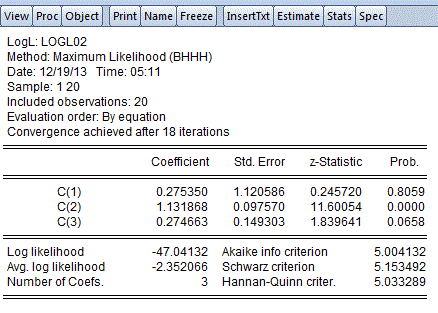
Estimating the model, as before, we obtain the following MLE output:

A quick check of the "gradient summary" reveals that the estimates correspond to a maximum of the Log-Likelihood function.

Because this model was estimated after the previous one, the stored values for the coefficients are used as the initial values for this estimation. If we edit the coefficient series in the workfile, and set c(1), c(2) and c(3) to "1", this is what we get when we re-estimate the model:

The results (including the maximized Log-Likelihood value) are not affected by the choice of starting values for the maximization algorithm, which is encouraging. Hopefully, we've found the global maximum.

If we compare these results, that assume a model with Student-t errors, with the earlier ones that assumed normally distributed errors, we see that the biggest difference arises with the estimate of c(3). Why is this?

In this last output, c(3) corresponds to the parameter "h", and for the Student-t distribution with v degrees of freedom, the variance is (v /h) / (v - 2), as long as v > 2. So, here, the estimated variance of the errors is approximately 10.922, and the standard deviation is 3.305. In the results based on the assumption of normally distributed errors, c(3) corresponds to the standard deviation of the errors, and the point estimate is 2.413. These two estimates of the standard deviation of the errors are quite similar numerically. In fact, they are not significantly different - note that the standard error for c(3) in the LOGL01 output is 0.603, so a a 95% confidence interval covers the value 3.305.

Recall that as v becomes infinitely large the Student-t density becomes a normal density. So, what do you think will happen if you keep increasing the value assigned to ν in the LOGL02 

code? Altering the code so that ν = 300, we get the following results: 

You can see that the estimates of c(1) and c(2) now essentially match their counterparts when normal errors are assumed. Going through the calculation for the estimated standard deviation of the Student-t errors we get 2.4163 (compared with 2.4133 for normal errors). This all makes sense.

PART 3

Let’s suppose that we want to generalize our last model even further. As well as allowing for an error distribution with fat tails, let’s suppose that we want to allow for a particular form of heteroskedasticity: 

where α₁ and α₂ are unknown parameters, and z is another variable for which data are available.

Note that the special case of homoskedastic errors arises if α₂ = 0. If we equate this variance
expression with the Student-t variance given above, we obtain: 

or,

Now we can create a new object, and name it LOGL03. We can use the following code to set up the Log-Likelihood Function for our simple regression model with independent but heteroskedastic Student-t errors:

@logl LL3 
eps = y-c(1)-c(2)*x 
v=3 
h=v/((v-2)*@exp(c(3)+c(4)*z)) 
const=@gamma((v+1)/2)/(@sqrt(v*3.14159)*@gamma(v/2)) 
LL3 = log(const)+0.5*log(h)-((v+1)/2)*log(1+h*(eps^2/v)) 

This yields the following MLE output:

The parameter c(4) corresponds to α₂. From the associated z-statistic, we see that we can't reject the hypothesis that α₂ = 0. So, we'd conclude that in fact the errors are homoskedastic, rather than being heteroskedastic of this particular form.

As in many econometrics packages, the estimation of non-standard models by the method of Maximum Likelihood is quite straightforward. It's always important to check the gradients (and the values of the Log-Likelihood function), using different in initial values for the estimation algorithm, to ensure that you've globally maximized the likelihood. This can be tricky in models with a lot of parameters.

Finally, although this example used a very small sample, it's also important to keep in mind that the desirable properties of Maximum Likelihood estimation - such as consistency and asymptotic efficiency - require a large sample size.

Have fun!

© 2013, David E. Giles