Cointegrated at the Hips

Spring is sprung and wedding season is fast approaching. Indeed, some couples have already taken the plunge this Spring. On 28 April, the day before Will and Kate got hitched (sorry - before the Royal nuptials of  Prince William and Catherine Middleton), The Economist magazine's Daily Chart showed the average age at first marriage for males and for females in the United Kingdom, from 1890 to 2010. The piece that accompanied with the chart went under the jolly title of "The Royal We", and discussed trends in marriage ages with markers at various key royal wedding dates over the years.

Several features of the chart were pretty much as you'd anticipate:

• The average age for grooms exceeds that for brides.
• There were structural breaks around the end  of the First and Second World Wars.
• Since about 1970, the average marriage age has been trending upwards (from about 22 and 24 years of age for brides and grooms in 1970; to about 29 and 31 years of age, respectively, in 2010).

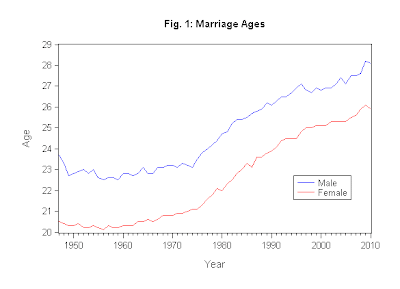
Always on the look-out for some new examples for my classes - especially ones that are a little bit "different" in their content - I thought it would be interesting to explore some similar data for U.S. pairings. The following chart shows the median age at first marriage for happy couples entering marriage for the first time between 1947 and 2010. The data are from the U.S. Census Bureau, and are available in the Excel workbook on the Data page that goes with this blog.

The general trend is similar to that for the U.K. over this period.

So, here's what I want to find out. Is there also some long-run equilibrating force that stops the ages of brides and grooms from "drifting apart" over time? Or, are we eventually going to end up with lots of old guys engaging in cradle snatching, or maybe even lots of "cougars" marrying young guys?

In econometric terms, we can re-phrase this question as:

"Are these two time-series cointegrated?"

Why don't we find out?

Here's the road map of where we're going:

1. Test each series to see if both of them are non-stationary, and have the same order of integration.
2. Make sure that the testing in step 1 takes account of the fact that there seems to be a break in the trend in 1975, in each series.
3. If both series are (say) I(1), then construct a VAR model for the 2 variables - this will require choosing the maximum lag-length.
4. Test the residuals of the VAR model to see if the errors are (a) independent; and (b) normally distributed.
5. Use Johansen's methodology to test if the 2 series are cointegrated.
6. In step 6, we'll have to again take account of the structural breaks in the trends of the data. To do this, we'll use the methods introduced by Johansen et al. (2000).

A couple of things to notice here before we get underway.

First, to test for unit roots in the presence of a structural break in the trend, I'm just going to use Perron's (1989) test. Be aware that there was an error in one of the key tables of critical values in his original paper, and this was later corrected by Perron and Vogelsang (1993). There are other tests that I could also use, but I want to put most of the emphasis on the cointegration testing with structural breaks, because this is less well-known in the applied literature.

Second, step 4 is pretty important for the following reason. When we move to Johansen's testing procedure it is based on the likelihood function. The latter is set up assuming independence and normality. So, if these conditions aren't satisfied we may have a problem with what then follows.

With those words of explanation, let's get underway. As usual, the EViews workfile for all of this is available on the Code page that accompanies this blog. Check out the "Read_Me" text object in the workfile for more details.

When I test the 2 time-series for their order of integration, with no allowance for the structural break (yet) this is what I get:

	ADF	Outcome	KPSS	Outcome
Male	-3.766	I(0)	0.185	I(1)
Female	-2.941	I(1)	0.207	I(1)

In the case of the ADF tests I've allowed for a drift and trend in the Dickey-Fuller regressions; and in the case of the KPSS tests the null is that the series is trend-stationary. So far, I'd conclude that the 2 series are I(1), but let's take account of the trend break in 1975. This is important, because the regular ADF test tends to "discover" unit roots that aren't actually there, when there are breaks in the data. Keep in mind that we can't test for cointegration if one or both the series is actually stationary.

The situation we're facing is about as tidy as it can get. There is a break in the trend at a single and easily determined point in the sample. This is Perron's Case 'B'.

For each time-series I'll do the following. I'll regress the series by OLS on an intercept, a linear trend variable (t in the EViews workfile), and a variable DT*. This last artificial variable takes the value zero up to and including 1975, and then the values 1, 2, 3,.....etc. to the end of the sample. The residuals from this first-stage regression are then tested for a unit root, using the ADF test with the "no drift-no trend" option for the Dickey-Fuller regression. This last point is important because the data have been filtered already for the drift and trend (with the break) in the first-stage regression.

The resulting ADF test statistics are -1.478 and -1.294 respectively for the MALES and FEMALES series. However, the usual critical values don't apply (even asymptotically) for this modified ADF test. Instead, we need to use Perron's asymptotic critical values (as corrected by Perron and Vogelsang (1993). The single break in the trend, in 1975, occurs at λ = 0.44 (44%) of the way through the sample. So, the 5% and 10% critical values are approximately -3.92 and -3.62 respectively. Clearly, we cannot reject the null of a unit root for either series.

Keep in mind that we have only 64 observations - not a very big sample. So, in a situation like this we might want to consider bootstrapping the critical value for the Perron-ADF tests, specific to our set of data and sample size. Not today, though, especially as the outcome of these last tests is not "borderline"!

O.K., so we've completed Step 2 in our road map. We're now in a position to test for cointegration between the male and female median first-marriage ages. When I fit a VAR model in the levels of the data, and use the usual information criteria (AIC, SIC, HQ, FPE) to determine the optimal maximum lag length, they all suggest just one period. That's O.K., but when we use the VAR model for cointegration testing we'll be differencing the data, so a second lag would be a good idea. An extra lag for the variables in the model isn't a bad idea here, anyway, to make sure that the residuals are "clean". So, I'm settling on a maximum lag length of k = 2 for the VAR model.

Recall Step 4 - apply some specification tests to this VAR model. Here are the results of testing for serial independence of the errors, using an LM test:

Lags	LM	p-value
1	7.169	0.127
2	1.866	0.760
3	7.200	0.126
4	7.903	0.095
5	1.592	0.810
6	8.589	0.072

When we test if the errors are normally distributed, we get the following results:

Variable	Jarque-Bera	d.f.	p-value
Male	1.945	2	0.378
Female	3.972	2	0.137
Joint	5.917	4	0.206

So far, so good. Now for the slightly trick part (Steps 5 and 6 on the path to cointegration bliss). We need to allow for those breaks in the trends of the male age and female age time-series when we implement Johansen's testing procedure. We're going to use the methods introduced by Johansen et al. (2000). Joyeux (2007) provides a very readable discussion of these methods, together with a nice application. Roselyne really knows her stuff, having done some of the seminal work on long-memory processes and fractional differencing, and I strongly recommend her paper to you.

What I need to do first, is to construct two dummy variables:

D_2,t = 0 (t = 1947, ...., 1975); = 1 (t = 1976, ..., 2010)

I_2,t = 1 (t = 1976) ; = 0 (elsewhere).

Then, when I set up the VAR model for the Johansen testing procedure, I include the following exogenous variables in the model:

• (Linear) trend
• D_2,t-k (where k, the maximum lag length, is 2 in our case)
• Trend*D_2,t-k
• I_2,t ; I_2,t-1; ......; I_2,(t-(k-1); where again, k = 2 in our case.

We then construct the usual Johansen trace test statistics.

This is what Johansen et al. (2000) call the H_l(r) test. The asymptotic distribution of the test is different from what it would usually be for the trace test. The asymptotic critical values depend on the proportion of the way through the sample that the break occurs (λ = 0.44 in our case); and on (p - r), where p is the number of variables under test p = 2, here), and r is the cointegrating rank being tested. So, for us,  r  = 0, 1.  Note that the test can be modified to allow for two structural breaks.

On the Code page for this blog there is a second EViews workfile, and an accompanying program file, that can be used to generate the asymptotic critical values for the H_l(r) test (and a second test), for various values of (p - r) and λ.

In EViews, I use option 4 as far as the deterministic trend specification is concerned. For our λ, the results of the H_l(r) cointegration tests are as follows:

No. of cointegrating equations	Hl(r)	10% Critical Value	5% Critical Value	Outcome
Zero	40.943	34.393	37.346	Reject
At Most 1	15.667	16.761	18.906	Do Not Reject

So, yes, the median ages at first marriage for U.S. males and females are found to be cointegrated.

A final observation. We saw that whether or not we allowed for the structural breaks in the data, we concluded that both of the time-series are I(1). However, if we don't allow for the structural breaks when undertaking the cointegration testing, it turns out that we come to the rather strange conclusion that there are two cointegrating relationships between the male and female marriage age series. You can easily check this yourself - see the EViews workfile. However, this result makes no sense! When we have only two I(1) time-series, the maximum number of cointegrating relationships is one - and if it's one, then the cointegrating vector is unique.

In other words, failing to use the appropriate methodology when testing for cointegration gives us the result we deserve: garbage! Here, doing the job properly really pays off.

Note: The links to the following references will be helpful only if your computer's IP address gives you access to the electronic versions of the publications in question. That's why a written References section is provided.

References

Johansen, S., R. Mosconi and B. Nielsen (2000). Cointegration analysis in the presence of structural breaks in the deterministic trend. Econometrics Journal, 3, 216-249.

Joyeux, R. (2007). How to deal with structural breaks in practical cointegration analysis? In B. B. Rao (ed.), Cointegration for the Applied Economist, Second Edition, Palgrave Macmillan, New York, 195-221.

Perron, P. (1989). The great crash, the oil price shock and the unit root hypothesis. Econometrica, 57, 1361-1401.

Perron, P. and T. J. Vogelsang (1993). The great crash, the oil price shock and the unit root hypothesis: erratum. Econometrica 61, 248-249.

© 2011, David E. Giles