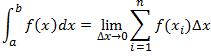My
recent post relating to maximum likelihood estimation of non-standard regression models in EViews included the case where the model's errors are independent Student-t distributed. In that example, the degrees of freedom for the Student-t distribution were assumed to be known. There was a good reason for making this assumption, as was spotted by Osman Dogan in his comment on that post.
If we relax this assumption and include the degrees of freedom parameter, v, of the t-distribution as another parameter that has to be estimated, then the likelihood function exhibits some unfortunate characteristics. Specifically, this function becomes unbounded at a boundary of the parameter space. Consequently, maximizing the likelihood function will generally result in us achieving only a local maximum, not a global maximum.
You might ask, "why would this matter?" Well, basically, if you want to be sure that your MLE achieves the good asymptotic properties that motivate us to use it in the first place, then you need to globally maximize the likelihood function.
I discussed this issue in some detail in an earlier post,
here.
In the context of the multiple regression model with independent Student-t errors with an unknown degrees of freedom parameter, these issues have been discussed fully by Fernandez and Steel (1999), for example. In particular, those authors show how a Bayesian approach to this estimation problem can overcome the difficulties associated with MLE here.
The problem is very reminiscent of the "incidental parameters" problem that arises widely in statistics, as well as in certain econometric estimation problems. Good examples of this general type of problem in econometrics include "switching regression" models; as well as models of markets that are in disequilibrium; and stochastic frontier production functions.
It's well known that a Bayesian approach is productive in the case of the "incidental parameters" problem, so it shouldn't be too surprising that it's also helpful with the Student-t regression model.
So, if you want to estimate a regression model with independent Student-t errors, and the degrees of freedom parameter associated with that distribution is unknown, then don't use maximum likelihood estimation! The Bayesian estimator discussed by Fernandez and Steel (1999) is one alternative. Pianto (2010) suggests a bootstrap estimator; and another possibility would be to consider method of moments estimation, which would result in estimates that are at least weakly consistent.
References
© 2013, David E. Giles