[Note: For an important update of this post, relating to EViews 9, see my 2015 post, here.]
Well, I finally got it done! Some of these posts take more time to prepare than you might think.
The first part of this discussion was covered in a (sort of!) recent post, in which I gave a brief description of Autoregressive Distributed Lag (ARDL) models, together with some historical perspective. Now it's time for us to get down to business and see how these models have come to play a very important role recently in the modelling of non-stationary time-series data.
Well, I finally got it done! Some of these posts take more time to prepare than you might think.
The first part of this discussion was covered in a (sort of!) recent post, in which I gave a brief description of Autoregressive Distributed Lag (ARDL) models, together with some historical perspective. Now it's time for us to get down to business and see how these models have come to play a very important role recently in the modelling of non-stationary time-series data.
In particular, we'll see how they're used to implement the so-called "Bounds Tests", to see if long-run relationships are present when we have a group of time-series, some of which may be stationary, while others are not. A detailed worked example, using EViews, is included.
First, recall that the basic form of an ARDL regression model is:
yt = β0 + β1yt-1 + .......+ βkyt-p + α0xt + α1xt-1 + α2xt-2 + ......... + αqxt-q + εt , (1)
where εt is a random "disturbance" term, which we'll assume is "well-behaved" in the usual sense. In particular, it will be serially independent.
yt = β0 + β1yt-1 + .......+ βkyt-p + α0xt + α1xt-1 + α2xt-2 + ......... + αqxt-q + εt , (1)
where εt is a random "disturbance" term, which we'll assume is "well-behaved" in the usual sense. In particular, it will be serially independent.
We're going to modify this model somewhat for our purposes here. Specifically, we'll work with a mixture of differences and levels of the data. The reasons for this will become apparent as we go along.
Let's suppose that we have a set of time-series variables, and we want to model the relationship between them, taking into account any unit roots and/or cointegration associated with the data. First, note that there are three straightforward situations that we're going to put to one side, because they can be dealt with in standard ways:
- We know that all of the series are I(0), and hence stationary. In this case, we can simply model the data in their levels, using OLS estimation, for example.
- We know that all of the series are integrated of the same order (e.g., I(1)), but they are not cointegrated. In this case, we can just (appropriately) difference each series, and estimate a standard regression model using OLS.
- We know that all of the series are integrated of the same order, and they are cointegrated. In this case, we can estimate two types of models: (i) An OLS regression model using the levels of the data. This will provide the long-run equilibrating relationship between the variables. (ii) An error-correction model (ECM), estimated by OLS. This model will represent the short-run dynamics of the relationship between the variables.
- Now, let's return to the more complicated situation mentioned above. Some of the variables in question may be stationary, some may be I(1) or even fractionally integrated, and there is also the possibility of cointegration among some of the I(1) variables. In other words, things just aren't as "clear cut" as in the three situations noted above.
What do we do in such cases if we want to model the data appropriately and extract both long-run and short-run relationships? This is where the ARDL model enters the picture.
The ARDL / Bounds Testing methodology of Pesaran and Shin (1999) and Pesaran et al. (2001) has a number of features that many researchers feel give it some advantages over conventional cointegration testing. For instance:
- It can be used with a mixture of I(0) and I(1) data.
- It involves just a single-equation set-up, making it simple to implement and interpret.
- Different variables can be assigned different lag-lengths as they enter the model.
We need a road map to help us. Here are the basic steps that we're going to follow (with details to be added below):
- Make sure than none of the variables are I(2), as such data will invalidate the methodology.
- Formulate an "unrestricted" error-correction model (ECM). This will be a particular type of ARDL model.
- Determine the appropriate lag structure for the model in step 2.
- Make sure that the errors of this model are serially independent.
- Make sure that the model is "dynamically stable".
- Perform a "Bounds Test" to see if there is evidence of a long-run relationship between the variables.
- If the outcome at step 6 is positive, estimate a long-run "levels model", as well as a separate "restricted" ECM.
- Use the results of the models estimated in step 7 to measure short-run dynamic effects, and the long-run equilibrating relationship between the variables.
We can see from the form of the generic ARDL model given in equation (1) above, that such models are characterised by having lags of the dependent variable, as well as lags (and perhaps the current value) of other variables, as the regressors. Let's suppose that there are three variables that we're interested in modelling: a dependent variable, y, and two other explanatory variables, x1 and x2. More generally, there will be (k + 1) variables - a dependent variable, and k other variables.
Before we start, let's recall what a conventional ECM for cointegrated data looks like. It would be of the form:
Δyt = β0 + Σ βiΔyt-i + ΣγjΔx1t-j + ΣδkΔx2t-k + φzt-1 + et ; (2)
Here, z, the "error-correction term", is the OLS residuals series from the long-run "cointegrating regression",
yt = α0 + α1x1t + α2x2t + vt ; (3)
The ranges of summation in (2) are from 1 to p, 0 to q1, and 0 to q2 respectively.
Now, back to our own analysis-
Δyt = β0 + Σ βiΔyt-i + ΣγjΔx1t-j + ΣδkΔx2t-k + φzt-1 + et ; (2)
Here, z, the "error-correction term", is the OLS residuals series from the long-run "cointegrating regression",
yt = α0 + α1x1t + α2x2t + vt ; (3)
The ranges of summation in (2) are from 1 to p, 0 to q1, and 0 to q2 respectively.
Now, back to our own analysis-
Step 1:
We can use the ADF and KPSS tests to check that none of the series we're working with are I(2).
Step 2:
We can use the ADF and KPSS tests to check that none of the series we're working with are I(2).
Step 2:
Formulate the following model:
Δyt = β0 + Σ βiΔyt-i + ΣγjΔx1t-j + ΣδkΔx2t-k + θ0yt-1 + θ1x1t-1 + θ2 x2t-1 + et ; (4)
Notice that this is almost like a traditional ECM. The difference is that we've now replaced the error-correction term, zt-1 with the terms yt-1, x1t-1, and x2t-1. From (3), we can see that the lagged residuals series would be zt-1 = (yt-1 - a0 - a1x1t-1 - a2x2t-1), where the a's are the OLS estimates of the α's. So, what we're doing in equation (4) is including the same lagged levels as we do in a regular ECM, but we're not restricting their coefficients.
This is why we might call equation (4) an "unrestricted ECM", or an "unconstrained ECM". Pesaran et al. (2001) call this a "conditional ECM".
Step 3:
The ranges of summation in the various terms in (4) are from 1 to p, 0 to q1, and 0 to q2 respectively.We need to select the appropriate values for the maximum lags, p, q1, and q2. Also, note that the "zero lags" on Δx1 and Δx2 may not necessarily be needed. Usually, these maximum lags are determined by using one or more of the "information criteria" - AIC, SC (BIC), HQ, etc. These criteria are based on a high log-likelihood value, with a "penalty" for including more lags to achieve this. The form of the penalty varies from one criterion to another. Each criterion starts with -2log(L), and then penalizes, so the smaller the value of an information criterion the better the result.Notice that this is almost like a traditional ECM. The difference is that we've now replaced the error-correction term, zt-1 with the terms yt-1, x1t-1, and x2t-1. From (3), we can see that the lagged residuals series would be zt-1 = (yt-1 - a0 - a1x1t-1 - a2x2t-1), where the a's are the OLS estimates of the α's. So, what we're doing in equation (4) is including the same lagged levels as we do in a regular ECM, but we're not restricting their coefficients.
This is why we might call equation (4) an "unrestricted ECM", or an "unconstrained ECM". Pesaran et al. (2001) call this a "conditional ECM".
Step 3:
I generally use the Schwarz (Bayes) criterion (SC), as it's a consistent model-selector. Some care has to be taken not to "over-select" the maximum lags, and I usually also pay some attention to the (apparent) significance of the coefficients in the model.
Step 4:
A key assumption in the ARDL / Bounds Testing methodology of Pesaran et al. (2001) is that the errors of equation (4) must be serially independent. As those authors note (p.308), this requirement may also be influential in our final choice of the maximum lags for the variables in the model.
Once an apparently suitable version of (4) has been estimated, we should use the LM test to test the null hypothesis that the errors are serially independent, against the alternative hypothesis that the errors are (either) AR(m) or MA(m), for m = 1, 2, 3,...., etc.
We have a model with an autoregressive structure, so we have to be sure that the model is "dynamically stable". For full details of what this means, see my recent post, When is an Autoregressive Model Dynamically Stable? What we need to do is to check that all of the inverse roots of the characteristic equation associated with our model lie strictly inside the unit circle. That recent post of mine showed how to trick EViews into giving us the information we want in order to check that this condition is satisfied. I won't repeat that here.
Step 6:
Now we're ready to perform the "Bounds Testing"!
Here's equation (4), again:
Δyt = β0 + Σ βiΔyt-i + ΣγjΔx1t-j + ΣδkΔx2t-k + θ0yt-1 + θ1x1t-1 + θ2 x2t-1 + et ; (4)
All that we're going to do is preform an "F-test" of the hypothesis, H0: θ0 = θ1 = θ2 = 0 ; against the alternative that H0 is not true. Simple enough - but why are we doing this?
As in conventional cointegration testing, we're testing for the absence of a long-run equilibrium relationship between the variables. This absence coincides with zero coefficients for yt-1, x1t-1 and x2t-1 in equation (4). A rejection of H0 implies that we have a long-run relationship.
There is a practical difficulty that has to be addressed when we conduct the F-test. The distribution of the test statistic is totally non-standard (and also depends on a "nuisance parameter", the cointegrating rank of the system) even in the asymptotic case where we have an infinitely large sample size. (This is somewhat akin to the situation with the Wald test when we test for Granger non-causality in the presence of non-stationary data. In that case, the problem is resolved by using the Toda-Yamamoto (1995) procedure, to ensure that the Wald test statistic is asymptotically chi-square, as discussed here.)
Exact critical values for the F-test aren't available for an arbitrary mix of I(0) and I(1) variables. However, Pesaran et al. (2001) supply bounds on the critical values for the asymptotic distribution of the F-statistic. For various situations (e.g., different numbers of variables, (k + 1)), they give lower and upper bounds on the critical values. In each case, the lower bound is based on the assumption that all of the variables are I(0), and the upper bound is based on the assumption that all of the variables are I(1). In fact, the truth may be somewhere in between these two polar extremes.
If the computed F-statistic falls below the lower bound we would conclude that the variables are I(0), so no cointegration is possible, by definition. If the F-statistic exceeds the upper bound, we conclude that we have cointegration. Finally, if the F-statistic falls between the bounds, the test is inconclusive.
Does this remind you of the old Durbin-Watson test for serial independence? It should!
As a cross-check, we should also perform a "Bounds t-test" of H0 : θ0 = 0, against H1 : θ0 < 0. If the t-statistic for yt-1 in equation (4) is greater than the "I(1) bound" tabulated by Pesaran et al. (2001; pp.303-304), this would support the conclusion that there is a long-run relationship between the variables. If the t-statistic is less than the "I(0) bound", we'd conclude that the data are all stationary.
Step 7:
Assuming that the bounds test leads to the conclusion of cointegration, we can meaningfully estimate the long-run equilibrium relationship between the variables:
yt = α0 + α1x1t + α2x2t + vt ; (5)
as well as the usual ECM:
Δyt = β0 + Σ βiΔyt-i + ΣγjΔx1t-j + ΣδkΔx2t-k + φzt-1 + et ; (6)
where zt-1 = (yt-1 -a0 - a1x1t-1 - a2x2t-1), and the a's are the OLS estimates of the α's in (5).
Step 8:
We can "extract" long-run effects from the unrestricted ECM. Looking back at equation (4), and noting that at a long-run equilibrium, Δyt = 0, Δx1t = Δx2t = 0, we see that the long-run coefficients for x1 and x2 are -(θ1/ θ0) and -(θ2/ θ0) respectively.
An Example:
Now we're ready to look at a very simple empirical example. I'm going to use the data for U.S. and European natural gas prices that I made available as a second example in my post, Testing for Granger Causality. I didn't go through the details of testing for Granger causality with that set of data, but I mentioned near the end of the post, and the EViews file (which included a "read_me" object with comments about the results) is there on the code page for this blog (dated 29 April, 2011).
If you look back at that earlier file, you'll find that I used the Toda-Yamamoto (1995) testing procedure to determine that there is Granger causality running from the U.S. series to the European series, but not vice versa.
A new EViews file that uses the same data for our ARDL modelling is available on the code page, under the date for the current post. The data for the two time-series we'll be using are also available on the data page for this blog. The data are monthly, from 1995(01) to 2011(03). In terms of the notation that was introduced earlier, we have (k + 1) = 2 variables, so k = 1 when it comes to the bounds testing.
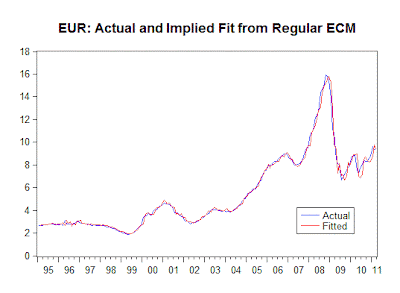
Here's a plot of the data we'll be using (remember that you can enlarge most of these inserts by clicking on them):
To complete Step 1, we need to check that neither of our time-series are I(2). Applying the ADF test to the levels of EUR and US, the p-values are 0.53 and 0.10 respectively. Applying the test to the first-differences of the series, the p-values are both 0.00. (The lag-lengths for the ADF regressions were chosen using the Schwarz criterion, SC.) Clearly, neither series is I(2).
Applying the KPSS test we reject the null of stationarity, even at the 1% significance level, for both EUR and US, but cannot reject the null of I(1) against I(2). The p-value of 10% for the ADF test of I(1) vs. I(0) for the EUR series may leave us wondering if that series is stationary, or not. You'll know that apparent "conflicts" between the outcomes of tests such as these are very common in practice.
This is a great illustration of how the ARDL / Bounds Testing methodology can help us. In order for standard cointegration testing (such as that of Engle and Granger, or Johansen) to make any sense, we must be really sure that all of the series are integrated of the same order. In this instance, you might not be feeling totally sure that this is the case.
Step 2 is straightforward. Given that the Granger causality testing associated with my earlier post suggested that there is causality from US to EUR (but not vice versa), ΔEUR is going to be the dependent variable in my unrestricted ECM:
ΔEURt = β0 + Σ βiΔEURt-i + ΣγjΔUSt-j + θ0EURt-1 + θ1USt-1 + et ; (5)
That's Step 2 out of the way!
To implement the information criteria for selecting the lag-lengths in an time-efficient way, I "tricked" EViews into providing lots of them at once by doing the following. I estimated a 1-equation VAR model for ΔEURt and I supplied the intercept, EURt-1, USt-1, and a fixed number of lags of ΔUSt as exogenous regressors. For example, when the fixed number of lags on ΔUSt was zero, here's how I specified the VAR:
After estimating this model, I then chose VIEW, LAG STRUCTURE, LAG LENGTH CRITERIA:
I then repeated this by adding ΔUSt-1 to the list of exogenous variables, and got the following results:
which resulted in the following information criteria values:

Looking at the SC values in these three tables of results, we see that a maximum lag of 4 is suggested for ΔEURt. (The AIC values suggest that 8 lags of ΔEURt may be appropriate, but some experimentation with this was not fruitful.)
There is virtually no difference between the SC values for the case where the model includes just USt as a regressor (0.8714), and the case where just ΔUSt-1 is included (0.8718). To get some dynamics into the model, I'm going to go with the latter case.
With Step 3 completed, and with this lag specification in mind, let's now look at the estimated unrestricted ECM:
Step 4 involves checking that the errors of this model are serially independent. Selecting VIEW, RESIDUAL DIAGNOSTICS, SERIAL CORRELATION LM TEST, I get the following results:
m LM p-value
1 0.079 0.779
2 2.878 0.237
3 5.380 0.146
4 11.753 0.019
O.K., we have a problem with serial correlation! To deal with it, I experimented with one or two additional lags of the dependent variable as regressors, and ended up with the following specification for the unrestricted ECM:
The serial independence results now look much more satisfactory:
m LM p-value
1 0.013 0.911
2 3.337 0.189
3 5.183 0.159
4 7.989 0.092
5 8.473 0.132
6 11.023 0.088
7 12.270 0.092
8 12.334 0.137
Next, Step 5 involves checking the dynamic stability of this ARDL model. Here are the inverse roots of the associated characteristic equation:
All seems to be well - these roots are all inside the unit circle.
Before proceeding to the Bounds Testing, let's take a look at the "fit" of our unrestricted ECM. The "Actual / Fitted / Residuals" plot looks like this:
When we "unscramble" these results, and look at the fit of the model in terms of explaining the level of EUR itself, rather than ΔEUR, things look pretty good:
We're now ready for Step 6 - the Bounds Test itself. We want to test if the coefficients of both EUR(-1) and US(-1) are zero in our estimated model (repeated below):
The associated F-test is obtained as follows:
With the result:
The value of our F-statistic is 5.827, and we have (k + 1) = 2 variables (EUR and US) in our model. So, when we go to the Bounds Test tables of critical values, we have k = 1.
Table CI (iii) on p.300 of Pesaran et al. (2001) is the relevant table for us to use here. We haven't constrained the intercept of our model, and there is no linear trend term included in the ECM. The lower and upper bounds for the F-test statistic at the 10%, 5%, and 1% significance levels are [4.04 , 4.78], [4.94 , 5.73], and [6.84 , 7.84] respectively.
As the value of our F-statistic exceeds the upper bound at the 5% significance level, we can conclude that there is evidence of a long-run relationship between the two time-series (at this level of significance or greater).
In addition, the t-statistic on EUR(-1) is -2.926. When we look at Table CII (iii) on p.303 of Pesaran et al. (2001), we find that the I(0) and I(1) bounds for the t-statistic at the 10%, 5%, and 1% significance levels are [-2.57 , -2.91], [-2.86 , -3.22], and [-3.43 , -3.82] respectively. At least at the 10% significance level, this result reinforces our conclusion that there is a long-run relationship between EUR and US.
So, here we are at Step 7 and Step 8.
Recalling our preferred unrestricted ECM:
we see that the long-run multiplier between US and EUR is -(0.047134 / (-0.030804)) = 1.53. In the long run, an increase of 1 unit in US will lead to an increase of 1.53 units in EUR.
If we estimate the levels model,
EURt = α0 + α1USt + vt ,
by OLS, and construct the residuals series, {zt}, we can fit a regular (restricted) ECM:
Notice that the coefficient of the error-correction term, zt-1, is negative and very significant. This is what we'd expect if there is cointegration between EUR and US. The magnitude of this coefficient implies that nearly 3% of any disequilibrium between EUR and US is corrected within one period (one month).
This final ECM is dynamically stable:
As none of the roots lie on the X (real) axis, it's clear that we have three complex conjugate pairs of roots. Accordingly, the short-run dynamics associated with the model are quite complicated. This can be seen if we consider the impulse response function associated with a "shock" of one (sample) standard deviation:
Finally, the within-sample fit (in terms of the levels of EUR) is exceptionally good:
In fact, the simple correlations between EUR and the "fitted" EUR series from the unrestricted and regular ECM's are each 0.994, and the correlation between the two fitted series is 0.9999.
So, there we have it - bounds testing with an ARDL model.
[Note: For an important update of this post, relating to EViews 9, see my 2015 post, here.]
Pesaran, M. H. and Y. Shin, 1999. An autoregressive distributed lag modelling approach to cointegration analysis. Chapter 11 in S. Strom (ed.), Econometrics and Economic Theory in the 20th Century: The Ragnar Frisch Centennial Symposium. Cambridge University Press, Cambridge. (Discussion Paper version.)
Pesaran, M. H., Shin, Y. and Smith, R. J., 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics, 16, 289–326.
Toda, H. Y and T. Yamamoto (1995). Statistical inferences in vector autoregressions with possibly integrated processes. Journal of Econometrics, 66, 225-250.
© 2013, David E. Giles















Great post! What is the preferred method for computing z? You show using a levels-on-levels OLS, but you also mention that the long run parameters can be estimated from the unrestricted ECM (i.e. the ARDL model used for the bounds test). Is it appropriate to use these implied parameters to construct z as well?
ReplyDeleteThanks. Either way can be used. In this particular example you get virtually the same results.
DeleteHi Sir,
DeleteI find your post very useful. But I am a bit confused with what k should be. Since k is the number of regressors, in this case it should be 2 not 1, right? because you test both EUR(-1) and US(-1) = 0. Please explain this more .. for example if I have one more variables and i want to test EUR(-1) = US(-1) = X(-1) = 0, what will be my k_?
As I note in Step 6 (the first Step 8, not the one in the actual application), the number of variables is denoted k+1, not k. So k=1 is the correct number.
DeleteThank you so much for super fast reply. Now I understand. I have one more question. If the F test falls in the range between the critical value, then what would be next step? can we still proceed with Granger causality test, similar to when no cointegration is found?
DeleteIf you are interested in causality testing, then in his case I'd be cautious because of the "between the bounds" outcome in the ARDL model. If you now use the TY methodology for the causality testing you'll be safe, even if there are unit roots and perhaps cointegration.
DeleteThank you sir.
DeleteSo you are suggesting that I should use T-Y causality instead of standard granger causality test?
hi professor Dave.
DeleteI have seen in several papers that the construction of the error correction term is to include lag of dependent variables, as well as several more lags of independent variables. As in your case, you only regress this model.
EURt = α0 + α1USt + vt ,
Is it ok to add lag of EURt-1 and USt-1 to capture the long run relationship? Please explain, the more I read paper about this model, the more I get confused. Thank you sir.
Usually we would NOT include lags such as those in forming the ECT. The ECT is supposed to be based on the residuals from the long-run equilibrating relationship, so it wouldn't include any dynamic effects.
DeleteYes - I'm suggesting that you use T-Y.
DeleteDear Professor Dave,
DeleteI just have one more small question, is it ok to add time trend in equation 3? (yt = α0 + α1x1t + α2x2t + vt ). Because in my analysis, I find that none of the coefficients are significant but when I add time trend, i got better results.
Thanks and regards,
Yes, you certainly can. (If you were using the simple Engle-Granger two-step approach to testing for cointegration, then when you fit the long-run equilibrating relationship - which corresponds to eq. 3 - you can either include or not include a linear trend. Your choice on this point then affects the critical values that apply when testing the stationarity of the residuals at the second stage.)
DeleteHere, if you include an intercept, make sure that you use the correct table(s) for the tests - see Pesaran et al., 2001. The tables are clearly titled to guide you.
Thank you sir.
DeleteI am wondering when you will make another example with multiple regressors? still looking forward to reading it especially how to select appropriate lag lengths for each regressor.
Excellent post! Thank you for your time and effort in putting
ReplyDeletethem all together with an example.
You're welcome - it was fun!
DeleteI was looking for a way to perform this in Eviews and with no help on google, I have to use trial version of limdep. Anyway, thank you very much for that.
ReplyDeleteYou're welcome - I hope it helps.
DeleteThank you Professor Dave for the Eviews solution. You have used here data of monthly frequency with the span of less than 20 years. I was wondering whether we can use data of less than 20 years for cointegration (is there a rule of thumb on this?)and that whether using the data of monthly frequency produces different results when compared to the data using annual or quarterly frequency (I have read in some old papers that frequency doesn't matter for cointegration so just wanted to make sure whether this still holds).
ReplyDeleteHi - thanks for the comment. There's no hard and fast rule for this. Remember, this is just an illustration. I'd really like at least 20 years, regardless of the frequency. We do know that what's important is the "temporal span" of the data, not just the number of observations. So, 50 annual observations are better than 5 years of monthly data (60 observations). Yes, the results can be sensitive to the choice of frequency - partly because there may be seasonal unit roots and seasonal cointegration that's being ignored.
DeleteOne point to note is that if there ARE seasonal unit roots in my data (& I haven't tested for them - it's really messy with monthly data), then this will invalidate the bounds testing. Pesaran et al. are very clear on this point.
Thank you once again Professor Dave for the clarification.
DeleteDavid,
ReplyDeleteWhat I like about most, but not all of your posts, is that for some of us who studied
some econometrics as part of studying economics can read these posts and be glad we can still understand this.
Keep it up.
However I have to say I am a tad disappointed there was only one article I could publicise this week!!
Thanks! Busy week :-)
DeleteDave is this a monster post! Thank you so much.
ReplyDeleteThanks for the comment. Sorry it took so long to complete!
DeleteProfessor, thank you for the post.
ReplyDeleteWhile you gave a recipe, you were very light on the theory side. For example, you did not explain why the joint test does what Pesaran et al claimed. For example, if the joint test rejects, it could be the case that (1) only one of the equalities fails, or (2) all of them fail. It is not clear if one could conclude the same thing from different reasons of rejection. Also, you did not explain why the additional bound test on y(t-1) is even needed and what happens if this test does not reject.
Thanks for the comments. This is just a blog post - not a text book! Sorry if you considered it a recipe - that's the last thing I would want, as you can see from my earlier posts on that very thing.
DeleteI'll be writing more about ARDL models - maybe you'll find it more to your liking.
DG
Thanks, Professor. To be honest, I don't think they explained these questions sufficiently well in the paper. The paper is well cited, but I feel that this is an example where people used the method without really understanding.
DeleteFair comment. I think you`re right. Let`s see if I can address your concerns to some degree in the follow-up post.
Deletehello Professor, thank you for the post.
ReplyDeleteI have a doubt, I need to estimate determinants of inflation in Cape Verde, and I have 7 variables how can select the appropriate values for the maximum lags for the 7 variables in eviews
You don't say what sort of model you have in mind, or what size your sample is. However, the SIC criterion is likely to be helpful.
Deletemy sample size 252(montlhy 1992m1 to 2013m3) my doubt is how i can select the appropriate values for the maximum lags for the 7 variables for estimate the ARDL equation to bounds testing co-integration method
DeleteThere is a large section in this post that discusses this very point.
DeleteDear professor,
ReplyDeletegreat post! Please allow me a bit of nitpicking. Not that it matters for the outcome of the F-test, but instead of citing the critical values for the 1% level, you cited the ones for the 2.5%. In the Pesaran et al. (2001), p. 300 table, the reported critical values are [6.84-7.84]. Maybe it would be interesting next post to include a bootstrapping exercise for generating critical values for the bounds test in small samples?
Thanks for spotting that! I've made the correction. Thanks for the bootstrap suggestion too!
DeleteDear Professor, thank you for the nice post. I was sincerely wondering whether there is any restriction in ARDL model that stationarity of the dependent variable.
ReplyDeleteThere's no restriction - typically it will be I(1).
DeleteMaybe a silly question, but are all these variables in log form? Thanks for this post David, I can't wait for the next instalment.
ReplyDeleteTim Watson
Tim - thanks for the comment. No, in this case they were in the levels of the data, not the logs.
DeleteThank you so much Professor Dave for this enlightening discussion and illustration using E-views. I had been struggling for the past one month to understand the bound-testing approach with ARDL model, and your post has been really helpful for my ongoing PhD work.
ReplyDeleteOne small query: How do we interpret the short-run relationship between two time-series, using this approach to ARDL model?
Hi - assuming you have found cointegration and moved on to fit an ECM, then this is the model that represents the short-run dynamics. You extract the short-run info. in the same way you would from any ECM.
DeleteFor instance, in my last restricted ECM, the coefficient of the error-correction term is -0.029. (It should be negative, or it makes no sense). It's roughly 3% in absolute value, so this tells us the speed of adjustment, per period, that you we move back to the long-run equilibrium after a short-run shock.
Thank you so much for your post
DeleteIs there any case, the coefficient of the error-correction term in ECM is smaller than -1, for instance the coefficient of the error-correction = -1.25
Best regards,
That makes no sense - it implies that there is an "over-correction" towards equilibrium.
DeleteDear Professor Giles,
ReplyDeleteThank you for your post! I have been trying to figure out whether I could use Eviews to ARDL model. Is it possible to post your program file for reference. This would be most appreciated. Thank you in advance for help.
Master student.
There is no program file - none is needed. The workfile has already been posted - that's all you need.
DeleteDear Prof, if I have multiple independent variables, how should I go about conducting step 3, ie. find the optimal lag length for each variable. Thanks.
ReplyDeleteYou need to work your way systematically through the lag length options, taking account of (i) statistical significance; (ii)minimizing the SIC values. Once you have your preferred specification, check that there is no remaining autocorrelation. If there is, you'll need to lengthen the max. lags, even if the terms aren't significant.
DeleteDear Prof, thanks for your kind response. I have 4 independent variables, so I suppose I would have quite a handful of different combinations of lag numbers for each variable to solve? Do you mean that I should run regression for the most general equation i.e. 12 lags for each variable and remove the insignificant ones? If so, I am not too sure on how does the SIC value criteria comes in.
DeleteAnd are the lag terms for each variable strictly of running order i.e. 1,2,3,4,5. Or the insignificant lag terms could be removed?
And one more question, if I found indeed there exists a cointegrating relationship between the variables, which contains a mixture of I(1) and I(0) series, could I form the VECM equation using all the variables? All should I form the VECM using the I(1) variables, and put those of I(0) as exogenous variables?
Really appreciate your help. I could drop you a separate email if it's more convenient for you. Thanks.
If you look at the original papers on ARDL models and bounds testing you'll see that they set a max. lag length and then look at all possible combinations of lags within this constraint. The model with the smallest SIC is chosen. That will involve a lot of possible combinations. I suggested taking account of significance to reduce this set of possibilities. Start with lots of lags, and test down, not the opposite.
DeleteIf you find cointegration with the bounds testing you can then fit an ECM. If you fit a VECM, then if you are SURE that some of the variables are I(0), set them to be exogenous.
Thanks Prof.
DeleteAre we able to apply johansen cointegration test for a VAR-GRACH model in Eviews?
Not with with a few "clicks", as far as I'm aware. You'd have to program it - and I think you'll find that's the case with any of the usual packages.
DeleteHI
ReplyDeletesee the step 7, zt-1 = (a0 - a1x1t-1 - a2x2t-1) , can you please confirm if the yt-1 is missed by typo or it is not there by purpose.
and can you please suggest some literature to study too see the implications if there is a trend in the long run equation.
thanks
Hi - thanks for spotting the omission! I have corrected it.
DeleteThe issue of trend is discussed in the Pesaran et al. reference.
Thanks
DeleteHello Professor, thank you so much for the post. It was helpful for me
ReplyDeletePlease in the ARDL (Bounds tests) model, I should test the normality of errors, homoscedasticity, and autocorrelation or not.
Engineering student
You should definitely test for lack of autocorrelation (as I did in the example in this post). Normality is less important. Given that you're working with time-series data, heteroskedasticity is not likely to be a major problem, but ideally you should also test for this.
DeleteThank you very much for the post. I have been struggling with how to perform bound tests for some days but your detailed explanation has granted me understanding. I have one observation though: The statement - "The upper and lower bounds for the F-test statistic at the 10%, 5%, and 1% significance levels are [4.04 , 4.78], [4.94 , 5.73], and [6.84 , 7.84] respectively". I think should read "Lower and Upper bounds". Thank you.
ReplyDeleteThanks - fixed.
DeleteThank you for the post. Please do you know how to run the bound test on STATA because I do not use EVIEWS in my university. Thank you
ReplyDeleteIf you look at what I've described, you'll see that all you have to be able to do is: (1) run an appropriate OLS regression; and (2) perform an F-test (but use the Non-standard "bounds" critical values). You can do that with any econometrics or statistics package.
DeleteThank you. I have a problem with interpreting a variable. *D(EUR(-1))* does this mean difference of lagged one variable or lag of first difference? Thank you
DeleteThe way it's written, it means the difference of the lagged variable. But the 2 things you've mentioned are identical to each other!
DeleteSee Narayan and Smyth (2005). they provide exact critical values for up to 80 observations
ReplyDeleteThanks - but a full reference would be helpful so that I can check this. The usual searches didn't turn up what I was looking for.
DeleteNarayan, P.K., 2005. “The saving and investment nexus for china: evidence from cointegration tests”. Applied Economics 37, 1979-1990 : http://www.xn--nide-1wa.edu.tr/ckfinder_portal/userfiles/files/narayan.pdf
DeleteThanks for this empirical application - however, it seems that the critical values you refer to aren't derived in this paper, but are (apparently?) derived in a couple of unpublished 2004 discussion papers. I'll try and track them down. Or, you could help us all by emailing them to me directly at dgiles@uvic.ca .
DeleteAlso your original comment mentioned "Narayan and Smyth", but neither this paper, nor any of the papers referred to in it, have this authorship.
hello sir, thanks for this post. in my model lag become zero and if i add trend then value of sbc inceases. so in short run equation dependent variable only in left hand side?
ReplyDeletethanks in advance
Check for serial correlation - of different orders. I'm sure this will be a problem. Then add lags until this problem is dealt with, regardless of SBC values.
DeleteProf. Giles, you ended this post with promising "a second and more comprehensive illustrative example", which "will involve more variables in the model." I have looked through all subsequent posts of yours, but haven't found anything more on ARDL Bounds test. Did I accidentally overlook it, or have you not made it available yet? Thanks!
ReplyDeletePatience, patience........ I do have a full-time job! :-)
DeleteIf possible, I hope we can see another excellent example with at least three variables in the ARDL model in summer 2014. Thanks for your great post!
DeleteProf. Giles, thanks for this post. I have some questions, are there no dynamic variables in the long run model? Ex. lagged dependent varible? And when you estimate the error correstion terms from the residuals are they from a model whitout dynamic terms or from the ARDL? And if you got that you should use Xt, Xt-1 and only Xt-1 is significant can I remove Xt? Thanks!
ReplyDeleteHi - there are no lagged values in the long-run model. The residuals series used to construct the error correction term come from the long-run model. And teh answer to your last question is "yes".
DeleteDear prof, I remarked that the R squared of the model above in the example is(0.38) less than 60%. Is it good for a ardl model ?
ReplyDeleteThank you.
That's pretty good for ANY models in which the dependent variable is in first differences (not levels).
DeleteD.G.
Please Mr Giles could you suggest me the lower value of R squared from it i can accept the model (ARDL).
DeleteThank you so much!
There's no simple answer to this question, just as there's no "smallest value" that you'd be ha[[y with for any regression model. Don't get overly concerned about the R-squared value - it's one of the least important statistics in any regression output.
DeleteNow I like. I wish you long life dear professor
ReplyDeleteProf. Giles, before we test for Granger Causality (Step2 ), must it be true that the VAR model is appropriate? What if the 2 VAR equations are not significant? Can we still go ahead and test for Granger noncausality?
ReplyDeleteYou could, but it would make a lot more sense if we had a model that seemed to be "significant" to begin with.
DeleteThank you for the response. I have another question: When we calculate BIC, N=Total no. of observations. So, suppose we have 250 observations, an AR(0) model has N=250 & T=250, while an AR(1) model has N=250, but T=249. What about the ECM? Originally, say I have 250 observations. When I write the ECM, and use zero lags of the differenced variables, is N=250 or 249, since 1 observation has been lost due to differencing. Stata calculates BIC incorrectly, by assuming N=T. I know that you use EViews, but could you clarify to me what N ought to be in a regression equation expressed in first differences? Many thanks!
DeleteClearly, N=249 in this case.
DeleteProf. Giles, with regard to the above question about significance, I get that only the 3rd lag of gdp is significant in predicting exports of a particular commodity. Shall I reestimate the unconditional ECM using only the third lagged difference of gdp? Is this valid? I am wondering if all variables have to have the same number of lagged differences, and whether the third lag can be part of the ECM without having the first and second. Thanks.
DeleteYou can have different numbers of lags for different variables; and can omit "intervening" lags if this is suggested by lack of signficance.
DeleteDear Professor Giles,
ReplyDeleteI am wondering if the long-run coefficients for x1 and x2 should be -(θ1 / θ0) and -(θ2 / θ0) respectively in step 8. I have benefited a lot from your blog. Thank you so much.
Thanks - fixed some time ago.
DeletePlease Mr, Is it true that ardl model help to avoid the problem of collinearity?
ReplyDeleteNo, this is not true.
DeleteHello Professor Dave,
ReplyDeleteI have some questions. Can we can use ARDL approach for panel data ? If yes, I don't use step 4 because I have tried ARDL for panel, but I don't succeful.
All of p-value of each variables of ARDL (inclus delay variables ) are signficative ?
Thank you
Check out http://ideas.repec.org/p/aee/wpaper/0605.html
DeleteIsn't the Pooled Mean Group estimator simply an ARDL estimator for panels?
DeleteYes it is. See http://www.jstor.org/discover/10.2307/2670182?uid=3739400&uid=2&uid=3737720&uid=4&sid=21102854321811
DeleteBut this doesn't cover bounds testing.
Dear Prof. Giles,
ReplyDeleteNarayan (2005) has provided critical values for small sample sizes (30 - 80). These are F-statistics, for testing the existence of a long-run relationship. However, he hasn't provided t-statistics for the bounds test. Given that the t-statistic also has non-standard distribution, could you recommend either a source in the literature that provides these statistics (bounds) for small samples, or suggest a way to generate them?
Your posts are eagerly awaited
Thanks,
I'm afraid I don't have a reference for you. You could bootstrap your particular results.
Deletethank you so much Pr Dave Giles.
ReplyDeleteCan you extend your post through panel cointegrated model using ARDL method
again thanks a lot.
:-) I'll try and find the time - I do have a full-time job! ;-)
DeleteHi professor Giles,
ReplyDeletethank you very much for your very helpful posts. There's a little, confusion in my mind..I don't know if I missed it from your previous posts. If all the variables under consideration are found to be I(0), but presence of cointegration is detected, is it ok to use an ECM? thank you for your help.
If all of the series are I(0) then they CAN'T be cointegrated - by definition. So an ECM is not appropriate.
DeleteDear Professor Giles,
ReplyDeleteThank you very much for your post; it helped me a lot with my thesis research. I am testing the relationship between economic growth and different types of energy consumption for 21 OECD countries by using TY technique.
My question is if a bidirectional causality was found, would it mean that two equations would have to be examined separately - in one economic growth would be an endogenous variable, and energy consumption exogenous, and vice versa?
Thank you for your help!
Thanks for your comment. So now you have sorted out the causality and want to actually model the structural relationships? If so, then you need a 2-equation simultaneous equations model, and you need to estimate by 2SLS, or 3SLS, or FIML. Or any other I.V. estimator, for that matter.
DeleteDear Professor Giles,
ReplyDeleteThank you for your response. I have sorted out the causality. Since I was using the TY technique, the cointegration didn’t have much impact on determination of the direction of causality because the variables did not have to be integrated of the same order. For the countries where energy consumption and economic growth are integrated of different orders, I am modeling the structural relationship by using ARDL Bounds tests. Although all the series for which I am doing ARDL Bounds Tests have a unidirectional causality, I just wanted to know how the test would work in the case of bidirectional causality.
Thank you again for answering my question.
Best regards,
Daria
Hello Professor,
ReplyDeleteMy question is not related directly to ARDL model, but I am confused , and I need your help. Please in my ARDL model I estimated the impact of exchange rate in trade balance deficit, and I use foreign revenue as one of variables, is not a problem if trade balance and foreign revenue are not in the same curency.
Thank you so much.
Best Regards,
hi professor,
ReplyDeletecan we use ARDL if endogenity does exist b/w variables?
As long as the endogenous regressors are lagged, current.
DeleteWorthy sir
ReplyDeleteReally great effort. Thanks for your time that you spend for us.
Dear Professor Dave Giles,
ReplyDeleteI have just a question. Why in the ARDL model, in the technical estimation in Eview, we must use the difference each series for estimate?
Thank you very much.
Because they may be I(1).
DeleteThank You very much for your efforts! this is really clear and helpfull theoretically and practically.
ReplyDeleteOne more question please, are the johansen cointegration test compatible with this modeling? Can they give us more information about long-term relationships?
Thank you again Professor.
Thanks for the comment. Just keep in mind that the Johansen test is based on the presumption that all of the series are I(1). The ARDL approach doesn't require this,
DeleteDear Prof.,
ReplyDeletePlease forward me the link for ARDL-models Part-I.
It's right there in the second line of this post!
DeleteDear prof.,
ReplyDeleteThank you so much for the post. However i would like to know if we need to test the significance of the long-run multiplier before jumping to the conclusions i.e step number 7. In other words, how will i know that the long run elasticity estimates are significant? And especially when the long-run regression coefficients extrated from ARDL model are not significant?
You can construct a standard error for the long-run parameter using the delta method, and immediately check significance that way.
DeleteDear prof,
ReplyDeletetank for this useful explanations.
I use stata and i haven't ever use eviews, is it possible to perform ARDL test with Stata?
thanks you and I look forward.
Yes - all you need is a package that will estimate a linear regression model.
DeleteProfessor Giles,
ReplyDeleteThanks for the post, it's very useful. just a brief question. I have a 3-variable case. Bound test suggests that these variables are cointegrated. However one of the two independent variables appears to be insignificant (in the long-run part). Should I drop this variable from the long-run equation and re-do the exercise? and only include this variable in the short-run part?
No, I'd keep in the long-run model, despite its individual insignificance, if you've established that there's a long-run cointegrating relationship between the three variables.
DeleteDear prof,
ReplyDeleteThank you so much for your post. This is really helpfull theoretically and practically.
One more question please, I have a model with 4 independent variables: X1, X2, X3, X4. So, how I can estimate lag length with each other. Example, with X1, first using Var process, next estimate d(X1) with C d(Y) Y(-1) X1(-1) X2(-1) X3(-1) X4(-1) or d(x1) with C d(Y(-1)) Y(-1) X1(-1) X2(-1) X3(-1) X4(-1), and last using AIC, BIC to select the lag length for X1. In this post, you only estimate the lag length for Y. So, with independent variables, how can we do?
Thank you and I look forward.
Dear Prof. D.Giles
ReplyDeleteI have benefited so much from your blog. I have a following question
In Step 7 - equation (5) yt = α0 + α1x1t + α2x2t + zt - the long-run equilibrium relationship
Before constructing ECM model, we must estimate equation (5) to get z(t-1), but some papers mentioned that to test the long-run equilibrium relationship, equation (5*) was used
Δyt = β0 + Σ βiΔy(t-i) + ΣγjΔx1(t-j) + ΣδkΔx2(t-k) + zt (5*). They will estimate equation (5*) to get z(t-1) to construct ECM model
My question is that comparing between equation (5) and equation (5*), which one is true?
Thank you so much
An ECM always models the short-run dynamics, not the long-run equilibrating relationship.
DeleteFirst of all, thank you for this extremely helpful exercise you have done!
ReplyDeleteI would like to ask, if I may, what if the ARDL bound test seems to confirm the cointegration between two variables (test value is > critical even at 1% lvl), but the when I fit a restricted ECM, the coeficients of lagged residuals series is nor negative, nor siginificant - does this mean that there is no cointegration after all? Or does this mean that there is an error in the model? Is it OK to receive controversial results?
Also, what would you suggest: If a wanted to investigate the effects of one variable to a few other variables, is it best to create multiple ARDL models for 2 variables or should I create multiple ARDL models for all variables included in each of them and only changing the endogenous variable?
Thanks a lot in advance!
First - it sounds as if the model may be mis-specified - or there may be issues arising from structural breaks in the data.
DeleteSecond - you should include all variable in the ARDL model.
Dear Professor Giles,
ReplyDeletethank you so much for explaining the ARDL method and all your responses.
Best wishes.
You're very welcome - I'm glad it was helpful.
DeleteDear Professor Giles,
ReplyDeletethank you so mush for this helpful exercise!
i would like to ask , in step 5, if the var model does not satisfy the stability condition , what should i do ?
thanks in advance.
First, it's not a VAR model. If the stability condition isn't satisfied you're going to have to modify the model's specification, via the lag structure, until it is satisfied. If this fails, you're going to have to abandon the model.
DeleteHello everyone,
ReplyDeletei like this very helpful exercise.
It's possible, to do the same in R??? i couldn't use EViews....
Step 1 it's possible
Step 2 it's also possible to generate an ARDL-model in R
Step 3: the lag-structure won't be a problem
Step 4: it's ok
Step 5: okay, now it becomes tricky. how to proof the stability of the model in R?? Could i use Breusch-Gofrey-Test??
Step 6: i don't know, if there is something i can use in R......
Does anyone can help??
thanks!
Dear Professor Giles
ReplyDeletePlease be kind enough to explain how could we resolve serial correlation and heterskedasticity problems in ARDL estimation using Microfit 4.01?
Thanks in advance
Sorry - I'm not a Microfit user.
DeleteDear Professor Giles,
ReplyDeletesorry for that question: how to get the last graphic of your analysis (the graphic with the fitted an actual Euro-serie......) in Eviews???
Put the 2 series in a GROUP and select VIEW, GRAPH, etc.
DeleteDear Professor Giles,
Deletethanks for your answer.
One question about step 7:
I would like to estimate the long run relationship equation (no. 5) . how i get the a's ??? you say, the a's are the OLS estimates of the α's in (5)
Thanks!
Just estimate equation (5) by OLS - then the z series is the residual series from the estimated (5) - it's just the usual error-correction term.
DeleteDear professor Giles,
ReplyDeleteI am trying to estimate an ARDL model, where the dependent variable is I(1) y and some of the explanatory variables are I(1) and some are I(0). Assuming the dependent and the I(1) explanatory variables are cointegrated, is it correct to include the I(0) variables even in the long-run relationship? Or should I(0) variables go only in the ECM?
Best regards
It can go in the long-run relationship as well.
DeleteThank you very much.
DeleteDoes the coefficient of the lagged dependent variable in the CCEM have to be negative and significant (like for the error correction term in a standard ECM?). If it turns out positive (and significant) does this signal a problem with model specification?
Thank you.
Yes; and Yes.
DeleteIn step 6, you say "If the t-statistic for yt-1 in equation (4) is less than the "I(1) bound" tabulated by Pesaran et al. (2001; pp.303-304), this would support the conclusion that there is a long-run relationship between the variables. If the t-statistic is greater than the "I(0) bound", we'd conclude that the data are all stationary."
ReplyDeleteShould it not be the other way around, i.e., when the t-stat is above I(1) bound, the null of no-cointegration is rejected in favour of the alternate hypothesis that the variables are cointegrated, and when the t-stat is below the I(0) bound, there is not enough evidence to reject the null of no-cointegration, and we conclude that the data are all stationary.
Am I mistaken?
You are absolutely right - thanks for spotting this. The change has been made.
DeleteDear Dave Thanks for this very helpful post in showing how to implement the ARDL bounds method in Eviews. I am wondering whether you can help me with a question. Suppose you wanted to see whether there is bi-directional causality between y and x. So then you run delta(y) as the dependent variable in the ECM (with a particular lag structure, dummies and time trend) and you find that the ECM coefficient is negative and significant and that the F stat is also significant. This suggests that x "pulls" at y. Now suppose you run another ECM with delta(x) as the dependent variable and just suppose that the lag structure is different and perhaps you have different dummies with no time trend (in short a different ECM). But you get a significant ECM coefficient which is negative and a significant F. Does that allow you to conclude that there is bi-directional causality? Thanks so much!
ReplyDeleteWhy not just set up a VAR and test for non-causality using the Toda-Yamamoto methodology to allow for the non-stationarity (and possible cointegration) of your data?
DeleteDear Prof. Giles,
ReplyDeleteThank you for this post. it helped me a lot. but now i'm confused with bounds testing procedure. As long as i understood after selecting optimal lag lenght for the model. For example i have a model with 3 independent variables. Before reading your post i used to found optimal ardl model with mfit then i do wald test with e-views. so if we suppose that i found optimal lag as 3 but ardl model as (2,1,1,1). should i do wald test with 3 lags for all variables, or should i use specified lags as mfit provided?
Thanks in advance,!
Sorry, but I have no familiarity with mfit. However, I don't understand why you would go back and forth between 2 packages in this instance.
DeleteHi Professor.
ReplyDeleteThanks for this post. I am working on the relationship between energy consumption, employment and economic growth for Saudi Arabia using the production function framework. I would like to use ARDL Bounds testing to cointegration but the data on labor are only available from 1990 to 2012. It seems that the period is too short, is it possible to use ARDL approach?
I must say I'b be dubious about ARDL results based on such a short sample. You will be really limited with the lag structures you can examine, and you'll run the risk of badly "under-specifying" the model.
DeleteThanks Professor Giles
ReplyDeletei am waiting for Panel data ARDL procedure. any idea when you will post this topic.
best wishes
Sir Dave Giles.. will u please guide how to calculate standard errors and t-ratios of long run coefficients???
ReplyDeleteYou can use the delta method.
Deletethank you for very much Sir. please share procedure for that in eviews, i am trying it since last week :(
DeleteThere is a link to the EViews files given in the post! Also, see the other post here: http://davegiles.blogspot.ca/2014/01/an-ardl-add-in-for-eviews.html
Deletesir
ReplyDeletecan the 2nd order data can also be used for ardl?i mean if you have data sets in first order nd 2nd order both, can still be ardl used?
No - you can't have any I(2) variables.
Deletei would like to ask what i can do in this case ? if i have variable I(0) ,I(1) and I(2) ??
DeleteDear Professor Giles,
ReplyDeleteThank you so much for such a wonderful tutorial!
When we perform VAR order selection and the calculation of VAR in EViews, why are all the observations included in the process (it shows included observations = 195 which is equal to the number of observations in the data set)? I tried to replicate your results using Stata and got results that are very close to those from Eviews, but not exactly the same. I notice that the number of observations included in Stata decreases, depending on the number of lags included in the model, which I think is the source of discrepancy in the results.
Thanks so much in advance for your reply and thank you once again for this wonderful blog.
Tongyai
Tongyai - I have no idea what Stata is doing - I never use it.
DeleteDear Professor,
ReplyDeleteThe ARDL approach to co-integration is based on a single equation approach. According to Pesaran, to deal with cases where there may be more than one level relationship involving yt will require the computation of further tables of critical values. Do you know what these critical values be?
Thank you
Sara - no off hand. Sorry!
DeleteThank you for your post. Do you know if they have actually published these critical values? Thank you anyway.
DeleteSorry, but I don't know.
DeleteDear Professor Giles,
ReplyDeleteThanks a lot for this amazing post! It helped me a lot.
I am currently trying to estimate an ARDL model with multiple explanatory variables. Thus, I have problems with step 3 because EViews always states "Near singular matrix" whenever I include too many variables/lags. Do you have any advice on how to deal with this?
Thanks a lot for your amazing blog and all the help!
Best
Maximilian
Maximilian - thanks for the comment. You are simply running out of degrees of freedom - you need longer time-series.
Deleteit Dependent variable is I(0) then what abot ARDL. it is still valid or it breaks down?
ReplyDeleteDear Prof. Giles,
ReplyDeleteFirstly, thank you for uploading this post, it has been extremely useful as a guide when conducting my own ARDL bounds test.
I'm curious as to why you have chosen to test for serial correlation in the errors of the unrestricted ECM in step 4 to just 4 lags? Having looked around I haven't found any concrete rule regarding the number of lags to test, but did read elsewhere that 12 lags would be appropriate (without any justification) in this case as monthly data is being used. Is there a specific reason that you have tested up to 4 lags?
Thank you,
Jacob
No particular reason - this is just an illustration.
DeleteDear Dave,
ReplyDeleteI have two questions. The first one is that why empirical papers use the ARDL Bounds testing approach in more than one equation?
The second question is: I am applying the ARDL model for studying the role of energy in economic growth by incorporating employment and capital as conventional inputs. How can I cite your post as a reference?
Mounir - I'm afraid I don't understand your first question.
DeleteTo cite: David E. Giles, "ARDL Models - Part II - Bounds Tests", Econometrics Beat, 19 June 2013, http://davegiles.blogspot.com/2013/06/ardl-models-part-ii-bounds-tests.html
Dear Dave,
ReplyDeleteAre the results of the Bounds Test valid if in the VEC model the coefficient on the lagged dependent variable is statistically insignificant?
Yes, that shouldn't matter.
DeleteThis is a great post - thank you for writing this it is very useful and interesting.
ReplyDeleteThanks the post. For the example you give, shouldn't the LR multiplier be the US lag coefficient/ Eur lag coefficient (under steps 7 and 8)?
ReplyDeleteThanks for spotting that - now fixed.
DeleteDear Professor Giles,
ReplyDeleteThank you very much for your post.
As I am currently working on a study including a ARDL bound testing model with multiple variables I was wondering whether you have already posted your article on this topic on your blog?
Thanks again!
Philip - sorry, not yet!
DeleteThank you for your reply. Looking forward to it!
DeleteHey professor, thank you for the detailed analysis. I have a question, that can we use the estimates of level OLS as the long run parameter of independent variable ? Or should we have to apply the formula of division for estimating the LR parameter? or can both be used ?
ReplyDeleteWill really appreciate your answer.
You should use the ratio approach, based on the modified ECM. If you use the simple levels model, in my example, you get an estimated coefficient of about 0.842. However, this won't be valid unless both variables are I(1) and cointegrated.
DeleteAnother question Professor Dave,.
ReplyDeleteBy SBC criterion, the lag of my data should be 4, but can I use a different lag ? such as 3 ?
because when I use 4, my model is not cointegrated.
Thank you prof!
No, you should not use less than 4 in this case.
DeleteDo all the variables should use 4 lags or we can apply for only one variable ?
DeleteI've read that when we use only one lag for a variable it can make a miss specification for the model. Does it true ?
The variables can have different lag lengths. Often, all possible combinations of lags are considered and we choose the one that results in the lowest SIC/AIC value. It's much more serious to under-estimate the number of lags than to over-estimate.
Deletethanks professor, it's really helpful :)
DeleteSir, there is a small typological mistake. please update it.
ReplyDeleteSee in Step 2:......"From (3), we can see that the lagged residuals series would be zt-1 = (a0 - a1x1t-1 - a2x2t-1), where the a's are the OLS estimates of the α's."
It would be zt-1 = (yt-1 -a0 - a1x1t-1 - a2x2t-1).
Thanks very much - fixed.
DeleteThanks for your helpful post. In the restricted ECM estimation, is it necessary to worry about the value of R square? Yours is 0.37 and mine is also around that.
ReplyDeleteKewani
Kewnai - you expect a low R-squared with any regression in which the dependent variable is first-differenced.
Deletedear professor thanks for your post.... now i am working with ardl model and found out that there is long run relationship among my variable... then i am fitted an error correction term, the sign is negative and significant, however my difference lags variable became not significant as in the bound test... is that problems?
ReplyDeleteNot necessarily. The bounds test is using an unrestricted ECM, now you have a restricted one.
DeleteHi Professor Giles,
ReplyDeleteI have an ARDL where I believe one variable (X) impacts Y over the first historical period and then another variable (Z) impacts Y over the second half of the time-series. I have a baseline ECM and then a second model where I add a dummy to separate the historical period and then appropriate multiplicative terms (short and long-run of X and Z multiplied by year dummy). Is this appropriate in the ECM? The model fits better when including the interaction terms and makes sense if my hypothesis is true.
Thank you in advance for your insights.
Hi - I don't see any major problem with this off-hand. However, it's difficult to answer these sorts of questions without seeing the model, the data, etc., and I can't provide a free consulting service for these things. Sorry!
DeleteThank you so much for this awesome post!
ReplyDeleteBut I have 2 questions:
1. Why is equation yt-1 - a0 - a1*x1t-1 - a2*x2t-1 called restricted and equation θ0*yt-1 + θ1*x1t-1 + θ2*x2t-1 called unrestricted? Where is a restriction in the first equation and where is an "unrestriction" in the second one?Why are they so called? And why is it applied in ARDL?
2. Why at first did you estimate unrestricted ECM and after that restricted ECM. Why do we need to perform the latter if we cannot use restricted ECM for ARDL model?
1. The term "restricted" is used because the lags of the variables don't enter separately, with coefficients that are estimated without any restriction. Instead they enter as a linear combination - i.e. as the lag of the residual term.
Delete2. The unrestricted ECM is what is needed for the bounds testing to be appropriate. Once we have determined that we have cointegration, then this implies (from Granger's Representation Theorem) that a restricted ECM must exist. And that's what we're interested in. So, one version of the model is for testing; the other is for estimation.
Prof. Giles,
ReplyDeleteGreat post! Thank you!
I have a question about estimating the long run coefficients in an ARDL model since I find two different approaches in the empirical literature.
In some articles the authors estimate a long run model, after evidence of cointegration, like this:
yt = β0 + Σ βiyt-i + Σγjx1t-j + ΣδkΔx2t-k + et
For example here: http://www.lahoreschoolofeconomics.edu.pk/JOURNAL/LJE%20Vol15-%20No.12010/1%20Waliullah%20EDITED%20AC.pdf
After selecting the optimal number of lags they use the coefficients of this equation as long run estimates.
It is not clear to me, which coefficient of which lag I have to take as long run coefficient? Or do I take the coefficient of the level variable there and are the lags only used as control variables? Could you help me out?
And next, they construct et as being the ECM term in the restricted ARDL ECM to estimate the short run dynamics.
This is, in my eyes, different to your approach of calculating the long run coefficients from the unrestricted error correction model by dividing the coefficients there and taking et just from your yt = α0 + α1x1t + α2x2t + vt model.
In some articles authors use both approaches...
Could you please help me out and explain which approach to use for long run coefficients? And the coefficient of which lag or level in the long run model to use as long run coefficient?
Additionally could you explain to me why we can estimate the long run coefficients in your example from dividing -(θ1/ θ0) and -(θ2/ θ0)?
Thank you very much!
Richard - these are good questions, and I'll do a separate post to address them properly.
DeleteHello Sir,
ReplyDeleteThanks for this very detailed explanation of ARDL Bounds testing. I have a question to ask, i.e., isn't rejecting the presence of a unit root in the second difference of a given variable the only necessary and sufficient condition for the justification of application of ARDL approach. If this is the case why do we need to check for presence/absence of unit root in level data or after first difference. I understand that if all the variables under consideration are I(0) then they can't be co-integrated but that would itself be reflected in the acceptance of null of no co-integration as per the Wald test for level data variables. So why not to preform unit root test only for the second difference of the variables?
Nishant - good question. I'll do a brief post on this.
DeleteThanks for your prompt reply. I will look forward to your post.
DeleteSorry i am a bit lost on step 3 ...how did the result of estimated unrestricted ECM come ?
ReplyDeleteDo you mean in the general outline or in the illustrative application? You'll have to be more specific.
Deletethank you prof. but i got it now
DeleteSorry i got it
ReplyDeleteDear Prof, Thank you for the briefing and i was not sure how you come with the value of Z which fitted in the model in step 7 ...thank you
ReplyDelete