Autoregressive processes arise frequently in econometrics. For example, we might have a simple dynamic model of the form:
yt = β0 + β1yt-1 + εt ; εt ~ i.i.d.[0 , σ2] . (1)
Or, we might have a regression model in which everything is "standard", except that the errors follow an autoregressive process:
yt = β0 + β1xt + ut (2)
ut = ρ ut-1 + εt ; εt ~ i.i.d.[0 , σ2] .
In each of these examples a first-order autoregressive, or AR(1), process is involved.
Higher-order AR processes are also commonly used. Although most undergrad. econometrics students are familiar with the notion of "stationarity" in the context of an AR(1) process, often they're not aware of the conditions needed to ensure the stationarity of more general AR models. Let's take a look at this issue.
First, what do we mean by a stochastic process that's "stationary"?
There are several types of "stationarity". Here, I'm going to use what we call "weak stationarity" (or "covariance stationarity"). What this means is that the mean and variance of the process are both finite and must not depend on time; and the covariances between pairs of random values from the process can depend on how far apart the values are in time, but not the value of time itself.
let's go back to the model in (1) above, and see what we mean by "stationarity" in this simple case. Notice that if we lag the equation by one period, we get:
yt-1 = β0 + β1yt-2 + εt-1 ; εt-1 ~ i.i.d.[0 , σ2] . (3)
Now, use (3) to eliminate yt-1 from (1), yielding:
yt = β0 + β1 [ β0 + β1yt-2 + εt-1 ] + εt .
Now, keep doing this repeatedly, and we end up with:
yt = β0 [1 + β1 + β12 + β13 + .......] + [εt + β1 εt-1 + β12εt-2 + ....]
or,
yt = β0Σ( β1i ) + Σ( β1iεt-i ), (4)
where the range of summation is from zero to infinity in each case.
Given what we assumed about the εt values in equation (1), we see from (4) that:
- E[ yt ] = β0Σ( β1i ) = μ ; say
- var.[ yt ] = σ2 Σ( β12i)
- cov.[ εt , εs ] = 0 ; for all t ≠ s .
Now, recalling some simple high school math, we know that Σ( β1i ) converges to the finite limit (1 - β1)-1, if and only if |β1| < 1. That is, it converges if and only if β1 lies strictly inside the unit interval. If this condition holds, then both E[ yt ] and var.[ yt ] will be finite - and you can see that neither they nor the covariances depend on the value of 't'. This condition on the value of β1 ensures that the series, yt, is covariance stationary.
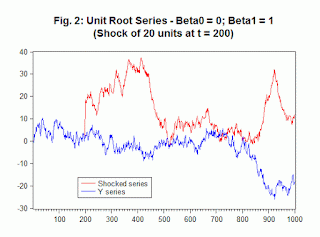
The case where β1 = 1 is termed the "unit root" case, for reasons that will become even more apparent below; and if | β1 | > 1, the yt series is "explosive". Let's see why this particular terminology is used. If the stationarity condition is not satisfied, then any "shock" to the yt series will lead to a subsequent time-path that has an unbounded mean and variance. On the other hand, if the process is stationary, then following such a "shock", the time-path for yt will eventually settle down to what it was previously. The shock will be "absorbed". For this reason we often say that non-stationary time-series have "long memories".
Let's see some examples of this. (Keep in mind that you can enlarge the charts by clicking on them.)
If you don't believe that this really is an explosive case, let's go out to t = 100:
The Eviews file that I used to create these charts is on the code page for this blog.
More generally, let's suppose that we have an AR(p) model, of the form:
yt = γ1 yt-1 + γ2 yt-2 + .......... + γp yt-p + εt ; εt ~ i.i.d.[0 , σ2]
Then the condition that must be satisfied in order that this model is dynamically stable is that all of the roots of the following so-called "characteristic equation"
1 - γ1 z - γ2 z2 - ..... - γp zp = 0 ,
lie strictly outside the unit circle.
It's worth noting that some authors define the characteristic equation as
zp - γ1 zp-1 - γ2 zp-2 - ...... - γp = 0 ,
and then the AR(p) process will be stationary if all of this equation's roots lie strictly inside the unit circle.
Let's go back to the AR(1) model - that is, set p = 1. In that case, the characteristic equation is
1 - γ1 z = 0.
Solving for z, we get z = 1 / γ1, so the stationarity condition is that |1 / γ1| > 1; or, equivalently, |γ1| < 1. This is exactly the condition that we saw above, now in our new notation.
Next, let's think about a series that is second-order autoregressive, or AR(2). In this case, the conditions that need to be satisfied to ensure stationarity of the series are more complicated. Suppose that our AR(2) model for Y is written as:
yt = γ1 yt-1 + γ2 yt-2 + εt ; εt ~ i.i.d.[0 , σ2] .
This model will be stationary (i.e., dynamically stable) if the roots of the characteristic equation,
1 - γ1z - γ2z2 = 0 ,
all lie strictly outside the unit circle. Equivalently, the roots of the equation,
z2 - γ1z - γ2 = 0,
must lie strictly inside the unit circle.
As I show in this attachment, when these roots are real (rather than complex) this is equivalent to requiring that the coefficients of the AR(2) model satisfy all of the following three conditions:
- (γ1 + γ2) < 1
- (γ2 - γ1) < 1
- |γ2| < 1
These three conditions allow us to depict the stationary and non-stationary regions of the parameter space in the following way:
Notice that this diagram also identifies the regions in the parameter space in which the series will respond to shocks in an oscillatory or non-oscillatory manner. The following two graphs illustrate this for two stationary AR(2) processes. In the first case, we have γ1 = 0.1 and γ2 = 0.8, so we are in the stationary/non-oscillatory region in the above chart:
The next case is for γ1 = 0.1 and γ2 = -0.8, so we are now in the stationary/oscillatory region of the parameter space:
A "blow-up" of these last two graphs follows:
Again, the EViews file that I used to create these data and charts is on the code page for this blog.
As we move to AR processes of higher order, the conditions that the parameters have to satisfy, to ensure that the process is stationary, become increasingly complicated to write down. However, the same basic principle applies - the roots of the associated "characteristic equation" must lie strictly outside the unit circle. Or, equivalently, the inverse roots must lie strictly inside that circle.
This is a condition that can be checked numerically, once we have values (estimates) of the coefficients of the AR process. It's just a matter of solving the characteristic equation for its roots, using these estimated values for the coefficients. Keep in mind that the roots will be functions of the coefficients, as we saw in the AR(1) and AR(2) cases.
In other words, even if it's really difficult to write down the formulae for the roots of the characteristic equation, it's a relatively simple matter to solve the equation for these roots, numerically. When we're estimating AR models using EViews, this gets done as a matter of course. In addition, you can request a diagram of the results, which is especially helpful if some of the roots are complex (rather than real).
To illustrate this, let's look at an example in which a restricted AR(4) model is used to "explain" the logarithm of real imports into Canada from the U.S.. The quarterly data exhibit a seasonal pattern, so seasonal dummy variables are included in the model:
Notice that the coefficient of the 1-period lagged value of the dependent variable is less than one in absolute value. So, we might be tempted to conclude that the model is dynamically stable. However, let's see what happens if we re-estimate the model using an apparently different, but mathematically equivalent, way:
The estimated coefficients and standard errors for the lagged values of the dependent variable in the first output are identical to the coefficients of the AR terms in the second output. Although the estimated intercept and dummy variable coefficients are different, in fact the model "fit" is identical in each case. You might guess this by observing that any of the reported statistics that are based on the residuals (e.g., R2, F-statistic, D-W statistic) are identical across the outputs.
However, the really interesting thing about the second set of results is that we now see the inverse roots of the characteristic equation associated with the restricted AR(4) process that we've used. This equation has four roots, of course, and it happens that ion this case there are two real roots, and a complex conjugate pair of roots. (More on the latter point below.) In particular, one of the real roots is one in value! Let's see this graphically:
Oh dear - we have a "unit root" situation associated with the dynamics of our AR(4) model. Note that I'm referring to the AR(4) process that describes how log(IMP) is related to lags of log(IMP). I'm not talking about the errors of that regression model.
Not surprisingly, when we "shock" the process by an amount equal to one sample standard deviation for the IMP variable, the shock does not die out. The effect just keeps on accumulating:
What can I do about this? Well, the log(IMP) data series itself is actually non-stationary, and I didn't take this into account. Using both the ADF test and the KPSS test, it's clear that the series is integrated of order one (i.e., I(1)). So, I need to first-difference the log(IMP) series to make it stationary, and then model it. Here's what I get:
In this case, the model for log(IMP) is dynamically stable, as we can see from the following diagram:
Once again, the characteristic equation has two real roots, and a complex conjugate pair of roots - and the inverted roots are all strictly inside the unit circle.
The EViews file for this example is on the code page for this blog, and the imports data are in a text file on then data page.
A few words of explanation may be in order with respect to the charts that show the inverse roots of the characteristic equation. These charts are in the form of an Argand diagram. They allow for the fact that some roots may be complex numbers, of the form z = (x +/ -iy), where the imaginary number, i, satisfies i2 = -1. The X-axis in those diagrams plots the real (x) part of z, and the Y-axis plots the imaginary (y) part of z. So, if a root is real, it will lie on the horizontal axis; but if it's complex, if will be located at the point (x , y).
What's the take-away message from all of this?
If you look back to the very first set of OLS results above, you'll see that the coefficient of log(IMP)t-1 was 0.8948. It was less than one in absolute value. However, once the full dynamic structure of the model was taken into account we found that the model was actually unstable. If you're estimating a higher-order AR process, you need to take special care when interpreting the magnitudes of the estimated coefficients!
Being able to see the values of the roots of the characteristic equation is enormously helpful when we're estimating an AR model (or, for that matter an MA or ARMA model). You certainly don't to inadvertently use a model that's dynamically unstable for forecasting purposes!
.
© 2013, David E. Giles














I tend to shy away from the advice to always difference when you have a unit root if your concern is primarily forecasting and you're not emphasizing hypothesis tests. The main reason is that when you generalize to a VAR, one variable having a unit root doesn't mean that all variables should be differenced. I could have equity prices and interest rates. On their own, the equity prices could be differenced, but the interest rates shouldn't. Together, the situation becomes more complicated.
ReplyDeleteI liked that you stress that it can be difficult to write down the formula for the roots even though it can be straightforward to find them numerically. I tried to use Matlab's symbolic math toolbox to derive them for even small size VARs on they look really complicated.
I will say that when I was learning about time series, I never had any idea what my Prof was talking about when she was talking about the characteristic equation since she didn't really explain how it comes about (or if she did, I didn't understand it). A matrix representation of the process makes it far more obvious, IMHO.
John - thanks for the constructive comments. I totally agree about the differencing, in general. I think my view on this will be clear from my other posts on VAR models, Granger causality, etc.
DeleteDG
Hello Prof. Giles,
ReplyDeleteUnder equation 4, where you have the first two moments and the autocovariance, since var(ax) = a^2*var(x), should it not be that var(y) = sigma^2 * sum(beta1 ^ 2) ?
Thanks!
JJ - thanks! Fixed!
DeleteProf. Giles,
ReplyDeleteIf I am estimating a regression model in difference or log difference form to address stationarity, is it still meaningful to put a trend variable? Thanks.
Only if the transformed data still exhibits a deterministic trend. This is unlikely after differencing.
DeletePro. Giles,
ReplyDeleteI estimated an ARIMA model, if one root of MA is 0.98, is there any problems to forecast with it? Thanks.
That depends on the other rots, including those associated with the AR process. You need to check the stationarity of the AR component and the invertibility of the full MA component. For example, if you have an MA(2) process, the invertibility condition are (Theta1+Thea2) < 1 & (Theta2 - Theta1) < 1 & |Theta2| < 1 . Just looking at one of the roots isn't enough.
DeleteDear Prof. Giles,
ReplyDeleteThanks for useful information. Can you please give the procedure how inverse roots of AR/MA polynomials can be obtained and graphed in Eviews software ? I really appreciate your help.
Thanks.
Once you've fitted the model, select "View", "ARMA Structure", "Roots", Graph".
DeleteThis is all in "HELP".
Thank you so much for prompt reply.
DeleteTrivial typo: In the repeated substitution expression that appears just above equation (4), the B0 term is missing. It is correctly included in equation (4), however, in the form of B0*B1^0.
ReplyDeleteThanks for spotting that. Now fixed.
DeleteGreat post. Does the cointegration concept apply to AR(m) model?
ReplyDeleteFor example, my goal is to use variable X(such as maket interest rate ) to forecast y (such as product pricing) by fitting AR(m) model as below
y_t=x_t*β+v_t
v_t=-φ_1* v_(t-1)-…-φ_m *v_(t-m)+ε_t
However I found out both x and y are stationary I(1). If I fit the AR model with my orginal data without differencing, what necessary steps I should take to verify x and y are cointegrated in the AR model? Does the cointegration concept apply to AR(m) model with nonstationary x and y? Thanks
If x and y are both I(1) then I think you meant to say that they are NON-stationary. In this case, the usual cointegration methods apply in this context.
DeleteHi Dr.Giles
ReplyDeleteIf I use the residual based two step Engle-Granger approach to prove cointegration for AR(m) model,
y_t=x_t*β+v_t
v_t=-φ_1* v_(t-1)-…-φ_m *v_(t-m)+e_t
which residual term, v_t or e_t, should I pick to test for stationarity in order to prove cointegration? Your answer is appreciated.
v_t
DeleteDear Prof Giles
ReplyDeleteNice blog Sir, My question is regarding the Image of Inverse roots of AR characteristics of Polynomials. As on of the observation is just on the boundary of circle. Could we consider this system stable enough to proceed further
That's analagous to the "unit root" case, and has the same adverse implications. The system isn't stationary.
Deletethanks prof.Giles, for your valuable and fruitful discussion on ARDL and related topics.
ReplyDeleteDear Professor Giles,
ReplyDeleteI run a VAR model in STATA, and find that is not stable. Noted the series are stationary.
What can be probable solution?
best regards,
Don't use STATA! (Just kidding). You'll have to adjust the maximum lag lengths.
DeleteDear Professor, thanks a lot for sharing this information. I have a doubt in the second characteristic equation (zp - γ1 zp-1 - γ2 zp-2 - ...... - γp = 0) of the AR model. The signs of the terms in the equation are different from what I observed in other texts (zp + γ1 zp-1 + γ2 zp-2 + ...... + γp = 0). Of course, the change in signs have significant impacts on assessing the behaviour of the process. Could you please share your comments on this?
ReplyDeleteIt's simply that there are 2 conventions. Then you either look at the roots, or the inverse roots. In the end it amounts to the same thing.
DeleteI really had a hard time trying to understand characteristic roots until now. Your explanations were so much clearer. Thank you Prof., please keep this going!
ReplyDeleteProf Giles, I will appreciate if you help in clarifying some concepts about implications of complex roots. What are the implications of complex roots in AR processes? Tsay says that they give rise to business cycles. This may be true with annual or quarterly aggregate economic series but how to interpret the complex roots of the AR/ARMA processes fitted to e.g daily data or non-macro series?
ReplyDeleteYes, the series will oscillate in this case. I wouldn't call it a "business cycle" in such cases.
DeleteWhere did y_{t-k} go on the right hand side of equation 4?
ReplyDeleteAs I said in the text, you just keep substituting. You replace y_(t-2) with beta_0 + beta_1*y_(t-3) + epsilon_(t-2); etc. You do this indefinitely. Note that the ranges of summation are from zero to infinity.
DeleteVery thorough and clear, can you please talk more about dynamic stability, I think that all stable processes are stationary, but vice-versa is not true.
ReplyDelete