Whenever we test the stationarity of our time-series data we use a "complete" historical time-series. That's to say, there can't be any "gaps" in the series,arising perhaps due to data observations that were not recorded, are contaminated, or are such extreme outliers that they are unbelievable and have to be discarded.
If observations are missing, for whatever reason, then we can't apply standard tests such as the Augmented-Dickey-Fuller (ADF) test, or the Kwiatowski, Phillips, Schmidt and Shin (KPSS) test.
Or can we?
Recently, one of my students ran into this very problem and asked me if I had any suggestions. As it happened, I did. A few years ago I worked with one of my then M.A. students, Kevin Ryan, on a closely related problem. We were interested in applying the ADF test to time-series data which exhibited a change in the recording frequency at some point in the sample.
For instance, suppose you have a series that was recorded only annually to begin with, but in more recent times the data were recorded quarterly. This situation is quite common, especially when you move to data outside of North America or Europe.
This is an example of a particular type of "missing data". In the annual-to-quarterly situation, during the early part of the sample three out of every four observations are "missing". Some methods for handling this in the case of the (non-augmented) DF test and Hall's (1989) I.V. test were first considered by Shin and Sarkar (1994a, 1994b). They suggested two specific "fixes", and investigated the consequences for distortion in the size (true significance level) of the tests.
What Kevin and I did was to investigate the merits of their suggested "fixes", and a third one discussed below, when applied to the ADF test. We also considered the implications for the power of the test, in addition to size distortion. Our results were published in Ryan and Giles (1998).
So, what are these three ways of dealing with the change of recording frequency, or the "missing" data points?
- "Close up" the gaps in the series. To consider a very simple example, suppose that we have data for y1, y2,....., yj-1, yj+1,...., yT (with yj missing). Then shift the (j+1)th observation back to the jth position, the (j+2)th observation back to the (j+1)th position, etc. The resulting series will then run "continuously" for (T-1) observations.
- Replace the missing observation(s) with the last recorded observation before the gap. For the example above, the series will then have T observations: y1, y2,....., yj-1, yj-1, yj+1,......., yT.
- Fill in a gap by linearly interpolating between the last recorded recorded observation before the gap, and the first recorded observation after the gap. For the example above, the series will then have T observations: y1, y2,....., yj-1, yj*, yj+1,......., yT . Here, yj* = yj-1 + (yj+1 - yj-1) / 2.
(The third method could be extended to a non-linear interpolation, especially if the gap involved several missing observations. We didn't pursue this idea.)
Kevin and I presented three sets of results, one analytical, and two based on an extensive simulation experiment which included situations in which up to a third of the series is "missing". The results can be summarized very briefly as follows:
- Asymptotics: The usual (non-standard) asymptotic distributions of the ADF test (under the "drift and trend", "drift but no trend", and "no drift and no trend" choices for the DF regression) are unchanged if any of the above three "fixes" are used.
- Size distortion: For a wide range of situations, Method 2 above results in the least distortion to the nominal significance levels of the ADF tests in finite samples.
- Power: In finite samples, Method 2 above results in the best size-adjusted power for the ADF tests.
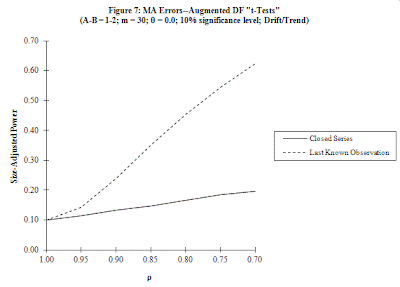
Here is just one illustrative (size-adjusted) power curve, to give the flavour of our results:
So, if you encounter a time-series in which one or more observations are "missing", for whatever reason, these results may help you in applying the ADF test in a sensible way.
There are at least two open research questions that I've not yet returned to:
There are at least two open research questions that I've not yet returned to:
- Do these results "carry over" to the Engle-Granger two-step test for cointegration (based on the use of the ADF test) when one or more of the series in question have values missing? My guess is that they probably do.
- What can be said about the properties of other related tests, such as the KPSS test, in these circumstances? My guess is that the asymptotics are unaffected. Byond that, I'm not sure.
References
Hall, A., 1989. Testing for a unit root in the presence of moving average errors. Biometrika, 76, 49-56.
Ryan, K. F. and D. E. A. Giles, 1998. Testing for unit roots in economic time-series with missing observations. In T. B. Fomby and R. C. Hill (eds.), Advances in Econometrics. JAI Press, Greenwich, CT, 203-242. (The final Working Paper version of the paper is available here, and the Figures are here.)
Shin, D. W. and S. Sarkar, 1994a. Unit roots for ARIMA(0,1,q) models with irregularly observed samples. Statistics and Pobability Letters, 19, 188-194.
Shin, D. W. and S. Sarkar, 1994b. Likelihood ratio type unit root tests for AR(1) models with nonconsecutive observations. Comunications in Statistics: Theory and Methods, 23, 1387-1397.
© 2012, David E. Giles
Dave -
ReplyDeleteThere is a similar and vastly understudied problem that I am currently working on with a grad student: dynamic panel data models with unobserved effects and unequally spaced panels. There is a little by David McKenzie in the context of pseudo-panels and little else. Unfortunately, with micro data, there is often missing data, or surveys that are irregularly spaced.
Thanks for the pointer - I'll check that out.
DeleteI wonder how much the results of ADF test in first differences are sensitive to the method applied. Regarding the second method, this imply that dy=0 when there is a missing observation, which means that the series are more likely to be stationary if there is a lot of missing values?
ReplyDeleteThen, your issue regarding Engle-Granger procedure is clearly interesting from my point, and I look forward to seeing a post on this.
Finally, I would like to ask you if you have an idea about the effect of these different methods on the estimation results of simple OLS or cointegration?
Thanks for all.
Thanks for the comment.
DeleteI have not looked at the I(2) vs. I(1) case
When it comes top missing data and simple OLS there is a vast literature on data imputation. Our work did not pretend to contribute to this.
I think that the reamining interesting issue is the usefulness of this approach when testing for cointegration.
Thanks for your reply! What I tried to say in my first observation is that in my mind if we replace a missing value by the last recorded observation, which corresponds to your second approach, then the series tends to pass more easily the stationnary test. But it's just a feeling I have from my own tests and i'm not sure that is really accurate.
DeleteRegarding the impact of these methods on OLS estimates, I just wanted to have your insights, but if you have some paper it's fine, thank you.
This comment has been removed by a blog administrator.
ReplyDeleteAnother big thing missing here is that some datasets have gaps by design. What about markets that are only open seasonally? Say 9 months a year. I have weekly data for each of those 9 months over a 15 year period. What might we do in that situation? Thanks!
ReplyDeleteHi Dave, thank you for the interesting research. How about the following way of dealing with missing data?
ReplyDeleteIf y[j] is missing in a sample of T observations, then the AR(1) model is estimated as,
y[2]=b0+b1*y[1]
y[3]=b0+b1*y[2]
...
y[j-1]=b0+b1*y[j-2]
y[j+2]=b0+b1*y[j+1]
...
y[T]=b0+b1*y[T-1]
Hi - sure, that would be another option. I don't know how well it would perform (in terms of size-distortion & power) relative to the other options I mentioned. It's similar to "closing the gap", but not quite the same.
Delete