Last month, in a post titled "Extracting the Correct Mean(ing) From the Data" (here), I discussed some aspects of the arithmetic, geometric, and harmonic sample means.
In a subsequent comment, I was asked if the geometric mean (GM) and harmonic mean (HM) are consistent estimators of E[X], the (arithmetic) mean of the population. My first reaction was that they are, but a little further reflection shows otherwise.
We know, from the weak law of large numbers (Khintchine's Theorem) that the AM is a weakly consistent estimator of E[X], provided that the sample values are uncorrelated and E[X] is itself finite. If we strengthen the "uncorrelated" requirement to "independent", then the AM converges almost surely to (is strongly consistent for E[X], by the strong law of large numbers. These results hold for any parent population whose mean is finite.
Now what about the GM and the HM?
The quickest way to show that they are not necessarily consistent for E[X] is to conduct a simulation experiment, and generate a counter-example. Remember that the GM is not defined for negative sample values, so let's make sure that we take this into account when choosing the population from which we sample.
I set up a simple Monte Carlo experiment, using EViews. The EViews workfile and program file can be found in the Code page that goes with this blog.
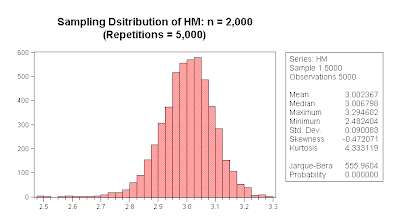
In the experiment, I used a parent population that was Chi-Square distributed with v = 5 degrees of freedom, so E[X] = 5. Simple random sampling was used, with 5,000 Monte Carlo replications, and with sample sizes of n = 50; 500; and 2,000. In each case, the simulated sampling distributions for GM and HM were constructed. By the time that we have n = 2,000 we should be getting close to the (large-n) asymptotic case.
There is a "READ ME" text-object in the EViews workfile that provides more details, but here are the simulated sampling distributions for the AM, GM, and HM when n = 2,000:
As expected, the mean of the sampling distribution for the AM is 5. The AM is unbiased, consistent, and asymptotically unbiased for E[X]. As far as the GM and HM are concerned, we have:
We see that these two sample statistics are each asymptotically biased (and hence inconsistent) estimators of E[X]. This is just for one situation, but all we needed was one counter-example!
Interestingly, at least for this example, the asymptotic means of the HM (= 3), GM (= 4) and AM (= 5) happen to satisfy the usual inequality for the sample averages themselves: HM < GM < AM.
© 2012, David E. Giles


There's a very simple way to prove analytically that the HM and the GM cannot be consistent estimators of E(x). Both can be written as
ReplyDeleteg^{-1}(1/n \sum g(x_i))
where g() is a non-linear function (eg the natural log for the GM).
Even if E[g(X)] exists (which may not), then it's different from g[E(x)], unless g() is linear.
Nick: Thanks for the comment. However, what you've established relates to the finite-sample bias. This doesn't say anything about the mean of the asymptotic distribution, and hence the asymptotic bias.
DeleteNot really. Lack of asymptotic bias is not the same thing as consistency. Let me be more explicit.
DeleteAs per one of the many versions of the WLLN, with iid observations the existence of E(x)=\mu implies that the sample average of X converges in probability to \mu.
Of course, the continuous mapping theorem implies that, if E(g(x)) also exists, then the sample average of g(x) will converge in probability to it. However, this limit will in general be different from g(\mu) unless g() is linear. As a consequence,
plim \frac{1}{n} \sum g(x_i) = E(g(x)) \ne g(E(x))
so
plim g^{-1}[\frac{1}{n} \sum g(x_i)] = \ne E(x)
which proves that g^{-1}(1/n \sum g(x_i)) is not consistent for E(x) from the definition of consistency (ie convergence in probability to the parameter of interest).
Jack: you're absolutely right, of course. Thanks for clarifying this!
DeleteDave: Wouldn't it make more sense to ask:
ReplyDelete1. Is the sample GM a consistent estimator of the population GM?
2. Is the sample HM a consistent estimator of the population HM?
Nick: Thanks for the comment. We know already that the answer to those questions is "yes". The question that was raised in the earlier comment was explicitly about estimators of E[X] - the arithmetic mena of the population.
ReplyDeleteI have one question about this convergence. If HM and the GM cannot be consistent estimators of E(x) and AM is, then AM,GM and HM cannot converge to the same finite number, yes? I read from somewhere that AM/GM converges to 1, and GM/HM converges to 1. Do the claims conflict with each other?
ReplyDeleteSorry, but what you read is simply wrong. As n goes to infinity, it is NOT the case that AM/GM converges to one, or that GM/HM converges to one. You can verify this really quickly with a couple of lines of code.
DeleteYou are right. Thanks a lot.
Delete