Last week I had a post titled More About Spurious Regressions. Implicitly, in that post, I assumed that readers would be familiar with terms such as "integrated data", "cointegration", "differencing", and "error correction model".
It tuns out that my assumption was wrong, as was apparent from the comment/request left on that post by one of my favourite readers (Anonymous), who wrote:
"The headlined subject of this post is of great interest to me -- a non-specialist. But this communication suffers greatly from the absence of a single real-world example of, e.g. "integrated" or "co-integrated" data, "differencing" (?), "error-correction model," etc. etc.
I'm not trying to be querulous. It's just that not all your interested readers are specialists. And the extra intellectual effort required to provide examples would help us..."
So, in response, let's see if what follows is of some help.
First, as requested, some basic definitions. These are a bit "rough and ready", and not intended to be definitive:
- Time: Tick, tock! That which passes, in a natural order,
& increasingly quickly as we get older. - Series:
The opposite of funny.A sequence of numerical values - Time-series: A series of values, ordered according to the passage of time, and usually measured at regular intervals. (
There's nothing funny about getting older.) - Differencing: The act of taking the difference between one value of a time-series and a previous value of that time-series.
- First-differencing: Differencing, in the case where "a previous value" is the immediately preceding value. That is, the creation of the time-series ΔYt = Yt - Yt-1, where Yt is the original time-series, and t = 1, 2, 3,......measures the passage of time.
- Stationary:
Not movingStrictly, "covariance stationary". The mean and variance of the time-series are constant (and finite); and the covariances between different values of the series depend only on the distance apart that the observations are, and not on the value of "time" (t) itself. - Non-stationary:
Moving.Just like it sounds! - Integrated: The opposite of "differenced".
- Order of integration: The number of time that the series has to be differenced in order to make it stationary. If that number is "one", then we;'ll say that the original series is "integrated of order one", or I(1), for short. A stationary time-series is I(0).
- Cointegrated: Suppose two or more time-series are each I(p), where p>0. Then these series are "cointegrated" if there exist one or more linear combinations of the series that are I(p-d), where d>0. In the simplest case, p = 1, and d = 1, so we are looking for linear combinations of I(1) series that are I(0). If p = 1 then if such a linear combination exists, it must be unique.
- Cointegrating regression: A linear OLS regression relating the levels of the non-stationary, but cointegrated, time-series. It represents the long-run equilibrating relationship between the variables.
- Error-correction model:
Spell-checker. A regression model that explains the short-term dynamics of the relationship between two or more non-stationary, but cointegrated, time-series variables. The model is constructed by using the differenced data (so that each variables is then stationary), as well as an "error-correction" term. The latter additional regressor is a lagged value of the residuals from the cointegrating relationship.
O.K., with that out of the way, let's turn to the requested examples. First some that illustrate the definitions given above, especially as they relate to "spurious regressions". Then, I'll provide the requested "real-world" example.
To begin with, here's a graph of a stationary, I(0), time-series:
It's actually a first-order autoregressive process (AR(1) process), with the autoregressive parameter set to 0.75. That is, Zt = 0.75Zt-1 + εt, where εt is i.i.d. N[0,1]. The series crosses its mean level (zero, in this case) frequently, which is typical of a stationary series.
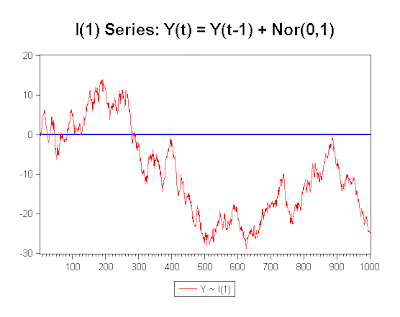
Now, here's an example of what an I(1) series can look like. You can see that the data have again been generated as an AR(1) process), but this time with the autoregressive parameter set to one in value. That's the "unit root" idea. The series "wanders about", crossing its mean level (zero) very few times. It can end up literally anywhere.
Now, let's see what happen when I "first-difference" this I(1) series. That is, I'll create a new series, of the form: ΔYt = (Yt - Yt-1); for t = 2, 3, ........
This new series is I(0) - it's stationary. You can see that it follows a time-path that's fundamentally different from that associated with the non-stationary series, Yt. Given the way that I generated Yt, this series for ΔYt is just a sequence of independent N[0,1] values. So, not surprisingly, there are very few observations that are greater than 3 in absolute value.
The X and Y series are different because a different string of values was used for the Normally distributed "error term" in the AR(1) models. You can see, though, that the series for X also crosses its mean level of zero very few times over the sample of 1,000 observations.
Now that we have two non-stationary, I(1), time-series, let's fit an OLS regression that "explains" Y in terms of X. Keep in mind that these two series were generated completely independently of each other. There is actually no relationship at all between Y and X!
However, that's not the impression that we get when we look at the OLS regression results below:
Even though the X and Y data have been generated so that they are actually independent of each other, the regression results suggest that there is a significant negative relationship between them. In addition, the R2 value suggests that X can explain 64% of the sample variation in the Y data; and the value of the DW statistic suggests that the errors in the model are positively autocorrelated.
These are the classic results that we associate with a "spurious regression".
In addition, if we test the regresssion residuals to see if the model's errors are normally distributed, the p-value for the Jarque-Bera test statistic is 0.006:
We strongly reject the hypothesis of normality, even tough in fact it is true. (The Y variable is normally distributed, so the OLS residuals will be normal too.) This result relating to the Jarque-Bera test is also typical of a spurious regression, as I discussed in a recent post.
If we were to interpret the results as telling us that we need to re-estimate the model, allowing for the autocorrelated errors, this is what we'd get as a result:
If we were to interpret the results as telling us that we need to re-estimate the model, allowing for the autocorrelated errors, this is what we'd get as a result:
The relationship between X and Y is no longer significant. Which is quite right!
However, this last model is still meaningless.
The absence of any meaningful relationship between Y and X is now fully revealed. Moreover, the known normality of the data is no longer rejected by the Jarque-Bera test.
Now let's consider some real economic data - to be specific, quarterly U.S. real private consumption expenditure and real personal disposable income. This is what these data look like for the period 1950Q1 to 1991Q4:
Both series are upward-trended, but are these deterministic trends, or stochastic trends (due to unit roots)? Maybe it's a bit of both?
Here's the correlogram for the consumption series - broken into 2 parts (with a gap), because a lot of lags are needed to see the "full picture":
The single spike in the partial autocorrelation function, coupled with the (initially) declining spikes in the autocorrelation function, suggest that the series follows an AR(1) process. When we see that the autocorrelations then start to increase again at higher lags, this suggests that the consumption series is non-stationary.
This is supported by applying the Augmented Dickey-Fuller (ADF) test (with drift and trend). The associated p-value is 0.6243. We would not reject the null hypothesis of a unit root at any reasonable significance level. The consumption series is I(1).
Similar results are obtained for the income series:
In this case, the p-value for the ADF test is 0.4768, and we again conclude that the series is I(1).
Now, suppose that we want to estimate a very basic consumption function, using these two time-series. We have to decide whether we can use the levels of the data, or whether we need to difference the data to allow for the fact that they are I(1).
The answer depends on whether or not the two series are cointegrated. If they aren't, then we should estimate a model with ΔCt as the dependent variable, and ΔYt as the primary regressor. We would probably also want to include lags of ΔYt and ΔCt as additional regressors. Differencing the data will ensure that all of the series being used are stationary, and so we will avoid having a "spurious regression".
On the other hand, if the consumption and income series are cointegrated, then we have two types of models that we can estimate legitimately:
- A model that uses the original data for Ct and Yt. Even though both series are I(1), the fact that they are cointegrated means that there is a linear combination of them that is stationary. Regressing Ct on Yt gives us this linear combination. This model will represent the long-run equilibrating relationship between consumption and income. Because only 2 variables are involved here, if a cointegrating relationship exists, then it must be unique. Again, we might want to include lagged values of Yt and/or Ct as additional regressors.
- An "error-correction model". As we saw in the definitions near the start of this post, this model would be of the general form: ΔCt = α1 + α2ΔYt + α3Rt-1 + ut , where Rt is the OLS residuals series from the "cointegrating regression" discussed in point 1 just above. A more general model would include lagged values of ΔCt and ΔYt as additional regressors. (More on this below.)
To test for cointegration, I'm simply going to use the Engle-Granger two-step approach. Yes, I know I can better than this, but it will suffice in the present context, especially as I have just two time-series. This will involve estimating a "cointegrating regression", and then testing if the residuals from this regression are non-stationary. A rejection of this null hypothesis, using the ADF test with MacKinnon's modified critical values, would lead us to conclude that consumption and income are cointegrated.
Here are the results that we get when we estimate a basic model of the first form above - the cointegrating regression:
The cointegrating regression ADF (CRADF) test statistic is -4.2398, and we reject the null hypothesis of "no cointegration" at the 1% significance level.
If we-estimate the contegrating regression with a linear time-trend added a regressor, the CRADF test statistic is -4.9736, and we come to the same conclusion, at the same level of significance. (In this case the estimated coefficient of the income variable is 0.9546.)
If we-estimate the contegrating regression with a linear time-trend added a regressor, the CRADF test statistic is -4.9736, and we come to the same conclusion, at the same level of significance. (In this case the estimated coefficient of the income variable is 0.9546.)
Given that we have established that there is cointegration between consumption and income, the last OLS results are perfectly meaningful, even though we are using levels of non-stationary data. The results from the cointegrating regression above imply a long-run marginal propensity to consume (mpc) of 0.877.
The residuals in this model are severely autocorrelated, and a more reasonable model is of the form:
The residuals in this model are severely autocorrelated, and a more reasonable model is of the form:
Now the residuals are serially independent, and the long-run mpc works out to be 0.870.
Now, let's consider an error-correction model, and explore the short-run dynamics of the relationship between consumption and income. Let Rt be the residuals series from the OLS (cointegrating) regression model, Ct = β1 + β2Yt + β3t + et. Then, our basic error-correction model will be:
ΔCt = α1 + α2ΔYt + α3Rt-1 + ut
In fact, what I've done is to start off with a slightly more general form of this model - one that also includes lagged values of ΔCt and ΔYt as additional regressors. I've then simplified the model by eliminating insignificant variables, and ensuring that there is no autocorrelation (up to fourth order) in the residuals. That is, I've used a "general-to-specific" modelling strategy, and here's what I ended up with:
I'm not saying this is "the very best" model, but it's reasonable for our present purposes. The estimated coefficient of the error-correction term is negative, and highly significant, as we'd expect if consumption and income are cointegrated.
If we "unscramble" the fitted values for the level (rather than the first-difference) of the consumption variable, and compare the fitted and actual values, the simple correlation is 0.99986:
If we "unscramble" the fitted values for the level (rather than the first-difference) of the consumption variable, and compare the fitted and actual values, the simple correlation is 0.99986:
The "residuals" expressed in the original levels of the data appear to be "white noise".
So, there's my "real-world" example. If you want to play around with yourself, the data are in a text file on the data page for this blog, and the EViews workfile that I used is on the code page.
© 2012, David E. Giles


















I think you meant "a first-order autoregressive process (AR(1) process), with the autoregressive parameter set to 0.75", not 0.5.
ReplyDeleteWhoops! Thanks - fixed!
ReplyDeleteCould you please elaborate on the long-run vs. short-run distinction at some point? I understand that in this simple model consumption depends only on today's income, so in the long-run equilibrium, C=a+b*Y, with b less than 1. When the residual R is large, that means that consumption is above equilibrium level, and since \alpha_{3} is negative, that will force consumption down, so the change in consumption should indeed be smaller.
ReplyDeleteCan do - more to come.
DeleteReally great post, especially for non-professionals. :)
ReplyDeleteThanks - glad it was helpful.
DeleteAmazing post for newbies like me! I'm actually saving your important post together with the example files in my computer because they are great for review and reference. Hopefully, I can read "back to basics" post in the future such as how to estimate supply and demand curve (simultaneous/system) or total factor productivity. Thanks!
ReplyDeleteThanks for the feedback - I'm pleased it was helpful.
DeleteThanks a lot for plenty of great posts! I’ve also read your post on panel unit root testing. Let’s assume I have a panel data model (sufficiently large T) and the appropriate test does not reject the null hypothesis of a unit root.
ReplyDeleteWould I then proceed in a similar way as described above, i.e. using panel cointegration tests and (potentially) formulating a panel error-correction model? Can you recommend any good (and not too technical) paper in this field?
Bests,
Tom
Tom: Yes, that's the way to proceed. The following paper from the St. Louis Fed. is very readable and may be helpful:
Deletehttp://research.stlouisfed.org/wp/2006/2006-050.pdf
Just interested. Below are two time series: the rate of unemployment and cumulative change in the real GDP per capita in the US from 1958 to 2010. (Kind of Okun's law. there is a break in 1978 associated with the change in GDP deflator definition. Question: are they cointegrated?
ReplyDelete9.547 9.6
9.575 9.3
7.065 5.8
5.742 4.6
5.286 4.6
5.183 5.1
5.268 5.5
5.598 6.0
5.416 5.8
4.905 4.7
4.031 4.0
4.531 4.2
5.327 4.5
5.895 4.9
6.496 5.4
6.780 5.6
6.494 6.1
6.911 6.9
6.725 7.5
6.773 6.9
5.157 5.6
4.605 5.3
4.919 5.5
5.497 6.2
5.664 7.0
5.944 7.2
6.543 7.5
8.555 9.6
9.323 9.7
7.092 7.6
6.904 7.2
5.347 5.9
5.377 6.1
6.459 7.1
6.806 7.7
7.477 8.5
5.905 5.6
4.216 4.9
5.065 5.6
5.672 6.0
5.414 5.0
3.931 3.5
3.686 3.6
4.134 3.8
3.614 3.8
4.667 4.5
5.642 5.2
6.309 5.6
6.382 5.6
7.090 6.7
6.267 5.5
5.341 5.5
6.424 6.8
The ADF test indicates that both series are stationary, so they can't be cointegrated.
DeleteThank you. Means the Rsq=0.9 is not biased?
DeleteMeans that you don't have a "spurious regtression" and you can interpret the R-squared in the usual way.
DeleteHowever, it doesn't necessarily mean that a simple regression of Y on X is the "best" model. Time for you to do some specification testing.
Right. The problem is that the residual 10% of the variability is likely from measurement errors and thus (considering the explicitly articulated by the BEA and BLS non-comparability of both time series) cannot be accurately caught by standard specification tests. For example, steps in the rate of unemployment and adjustments to the population controls (we use GDP per capita and thus divide by the population term) . Anyway, than you
DeleteProf. Dave, thank you so much for the excellent discussion. However, I have a quick question. You said "The ADF test indicates that both series are stationary, so they can't be cointegrated." What does that exactly mean? Does it mean that consumption and disposable income are not in a long-run relationship? If the answer is "yes", then how is the regression in level meaningful?
DeleteThe very definition of cointegration is as follows. If we have 2 or more series that are all integrated of order d (that is, they are all I(d)), and there exist one or more linear combinations of the series that are integrated of order (d-k), where k>0, then the I(d) series are "cointegrated". The most common case is where the series are all I(1), but a linear combination of them is I(0) (and hence stationary), then the series are cointegrated. However, if all of the series are I(0) to begin with, then any linear combination of them will also be I(0). This isn't cointegration - it's actually just the standard situation that we actually assume to be the case when we first learn about fitting a regression. We assume/pretend that we're in a stationary world. If we're not, then it makes no sense to estimate the coefficients, as they can't be constant.
DeleteThanks! Does that also mean that spurious regression is a minor problem in my panel model when I have additionally a lagged dependent variable as regressor on the rhs of my equation (given that the dependent variable and some other variables are integrated)?
ReplyDelete(Of course, in a panel model with fixed effects this could give rise to other problems...)
Kind regards,
Tom
Hello there! I want to ask you if it can exist a time-series that apparently is non-stationary and that it can”t be stationarised using differencing or log method or both at the same time or any other method.
ReplyDeleteAnd also, if it can exist a time-series that has been stationarised using first-differencing and after this procedure the correlogram shows no autocorrelation so no time-model can be applied on it. Thanks in advance!
Yes; and Yes.
ReplyDeleteok..very interesting these time-series are :)) but let me tell you this : I had a time-series of 20 cases from 1990 to 2009 concerning real private consumption expenditure; the series graph revealed that the time-series was non-stationary and the p-value for ADF test for the model with trend and intercept was 0,08 which was significant for a significance level of alpha=0,10 (or 10%) but not significant for an alpha of 5%. I considered the time-series to be stationary for an alpha of 0,10 and by visualizing the AF and PAF of the time-series correlogram I chose to estimate some regression modelslike AR(1), AR (2) and ARMA(1,1) and ARMA(2,2). Finally, I chose AR(1) model based on ”the best” R squared value, DW value, Jarque Berra p-value, AIC and SIC values. My question is : is this correct? I mean, is it correct to consider an alpha of 0,10 and thus concluding that my time-series is stationary having the p-value of ADF test below my considered alpha, and continuing specifing some models based on a non-differenced time-series?
ReplyDeleteRaluca: There's no right way or wrong way to interpret a p-value, or to choose a significance level. It's subjective. If YOU have in mind a significance level of 10%, then you'd reject the null hypothesis if your p-value is 8%. But in exactly the same context it would be perfectly OK for me to say that I have mind a 5% sig. level, so I would NOT reject the null hypothesis.
DeleteFor more on p-values, see http://davegiles.blogspot.com/2011/04/may-i-show-you-my-collection-of-p.html
This is extremely helpful. Are you planning doing a post on tests for multivariate cointegration (Johansen) relationships in the future? Your exposition is very clear and helps a lot with my studies.
ReplyDeleteThanks! You'll find some information in an earlier post at
ReplyDeletehttp://davegiles.blogspot.ca/2011/05/cointegrated-at-hips.html ,
but no doubt I'll do more in the near future.
this is helping, am an undergraduate student of economics, and sincerely speaking this is amazing. What i want to know is the generation of the error correction term, i av been battling with it for some times now, but av not been able to do it.
ReplyDeleteThanks for the comment. Suppose you have vaaibles Y and X, both of which are I(1) and they are cointegrated. You regress Y on X (and a constant), using OLS. Then you take the residuals series from thie "cointegrating regression". The lagged residuals series is the "error correction term" that you then include in the ECM.
DeleteUsually, we would use a one-period lag of the residuals, but there is nothing wrong with using a 2-period (or any-period) IN PLACE OF the one-period lag residuals series.
Thanks for this post. I'd appreciate if you could clarify the following issues I'm encountering about error correction models:
ReplyDelete1. You estimated the long-run equation using OLS. Shouldn't it be the FM-OLS under the cointreg option in EViews?
2. The long-run equation is often interpreted as a static relationship. Aren't the lags in the long-run equation, as you did above, inconsistent with that notion? Textbook examples usually show a contemporaneous relationship between the two series. Is there a way to address the autocorrelation problem which is usually present in the long-run equations without having to include lags (e.g. using HAC standard errors)?
3. Again, textbook examples (at least the undergrad books) show only bivariate cases for the Engle-Granger two-step approach. Is it still the right method to use in the case where the long-run equation has more than one explanatory variable?
4. Is it right to use variables outside the long-run equation in estimating the short-run equation? Conversely, is it right not to use the lagged differences of the explanatory variable in the short-run equation (say, because it is not significant)?
5. Can the ECM framework be used in the context of a simultaneous equation model where not all equations have error correction terms? For example, in your post about Estimating and Simulating SEMs, could we estimate the consumption and wage functions as ECMs while the investment equation remains estimated as usual?
Sorry for such lengthy queries!
Thanks for the questions/comments. Much appreciated.
ReplyDelete1. Using the fully modified OLS option would indeed have been better - I just wanted to keep it really simple here.
2. It's not that uncommon to include lags here. The HAC standard errors don't affect the coefficient estimates, of course. Using them will not address the main problem of the effect that the autocorrelation will have on the parameter estimates.
3. The EG method can be used with any number of variables - see the MacKInnon tables for critical values. If thee are just 2 variables and they are cointegrated, then the cointgegrating vector will be unique. This is no longer true when there are 3 or more variables. The Johansen methodology deals with this issue, among others.
If you have (say) 3 variables and you are testing for cointegration using the EG approach, you really need to check each possible choice of dependent variable. As I recall, there was early work by Dolado that indicated that you should then go with the cointegration results implied by the cointegrating regression with the highest R-squared.
4. First part - no, not really correct. Second part - that's fine.
5. Yes, you could certainly do this.
Sorry to be slow in responding!
Thank you for your response.
DeleteRegarding 4, What aspect of ECMs is one violating when variables not included in the cointegrating regression are included in the short-run eq.?
I'm quite confused after encountering papers that have variables in the short-run eq., which are not in the long-run eq.
For example in eq. 10 of G. de Brouwer & N. Ericsson (Modelling Inflation in Australia, JBES, Vol.16 No. 4, Oct. 1998), output gap (y^res) is included in the short-run eq. even if it is not in the long-run eq. The authors say that output gap, "may capture economically and statistically important behavior in prices, their effects are viewed as short-run and so are not included in the cointegration analysis."
That has always been my intuitive understanding of the error correction methodology. That is, factors that may have no effect on a variable in the long-run, could influence it in the short-run.
Another question is on whether it is appropriate to use say dlog(p,0,4) instead of the usual dlog(p) for the short-run specification. In this case, I'm using the 4th lagged of the res=p-(a+bx) instead of the 1st. I'm doing this because for the case of inflation, it is the yoy rate that we're interested in anyway and not the qoq rate. In the case of monthly data, I'm using dlog(p,0,12) and the 12th lag of the residual term.
Thanks!
John - good comments/questions, thanks. First, short run vs. long-run. Let's suppose that the "extra" variables that you think should be in the short-run equation, but not in the long-run relationship are all I(0). Then I don't see any propblem at all. However, what if you have an "extra short-run" variable that is I(1)? Then it really should have been included in the cointegration stage of the anlaysis, and the ECT that you'll have in the ECM will be mis-specified.
DeleteSecond question - it's fine to use a lag other than one for the ECT - for exactly the reasons you suggest.
Again, your reply is very much appreciated.
DeleteWhat I normally do is that when an I(1) variable is not significant in the long-run relationship, I try to see whether its I(0) transformation becomes significant in the short-run eq. So that probably rules out the possibility of including extra short-run variables that should be in the long-run eq.
Thanks!
John - that makes sense to me.
DeleteIs there a need to correct for autocorrelation in the residuals of the cointegrating regression? Wouldn't the OLS estimates of the regression be "super consistent" as long as cointegration exists? Am I right in saying that since we are not making any inference on the coefficients of the cointegrating regression, there is no need to correct for autocorrelation?
ReplyDeleteIN general, that's correct. However, in my example I was interested in the long-run relationship itself (beyond using it to test for cointegration). To get a sensible inference about the l.r.m.p.c. I really needed to allow for the autocorelation.
DeleteVector Error Correction Estimates
ReplyDeleteDate: 09/11/12 Time: 10:45
Sample (adjusted): 1972 2009
Included observations: 38 after adjustments
Standard errors in ( ) & t-statistics in [ ]
Error correction D(LNGDP) D(LNEG) D(LNSG) D(LNPG)
CointEq1 -0.868727 -0.003288 -0.096697 0.075553
(0.17306) (0.02349) (0.08538) (0.08363)
[-5.01992][-0.13999][-1.13257][ 0.90343]
D(LNGDP(-1)) 0.386149 -0.007050 0.026672 0.031272
(0.16926) (0.02297) (0.08351) (0.08180)
[ 2.28134][-0.30689][ 0.31939][ 0.38232]
D(LNEG(-1)) -6.118703 -0.392782 -0.494722 0.040937
(1.78393) (0.24210)(0.88012)(0.86209)
[-3.42989][-1.62238][-0.56211][ 0.04749]
D(LNSG(-1)) 0.168928 0.033797 0.063660 -0.086932
(0.37154) (0.05042) (0.18330) (0.17955)
[ 0.45467][ 0.67028][ 0.34730][-0.48418]
D(LNPG(-1)) -0.419299 -0.035227 -0.036414 -0.042079
(0.36482) (0.04951) (0.17999) (0.17630)
[-1.14932][-0.71149][-0.20231][-0.23868]
C 0.090502 0.009705 0.016354 0.024579
(0.02572) (0.00349) (0.01269) (0.01243)
[ 3.51846][ 2.78028][ 1.28873][ 1.97734]
Hello, need a professional advice here regarding VECM.
All variables are cointegrated, however the result of error correction term is not significant (the value is negative, but not significant). Since im a newbie on this, i dont know what seem to be the problem or how to correct it. thankkkss
There are several possible explanations for this, including:
Delete1. Are the data really cointegrated? For instance, did you deal with the issue of trends properly when applying the Johansen methodology? Are the errors Normally distributed - if not, the wrong likelihood function is used in the Johansen analysis.
2. Are you sure that all of the series have the same order of integration? Perhaps one of them is really I(2)?
3. Are there any structural breaks in the data? If so, this may impact on your tests for unit roots, your test for cointegration, and the specification of your VECM.
Prof Giles, to incorporate structural breaks in cointegration and VECM, is it enough to add a dummy variables for a specific year in the exogenous box on VAR, Cointegration, and VECM?
DeleteOften, that will be sufficient, depending on how "complicated" your break is.
Deleteit is a great post, for the last month em going through it for help coz this is exam season :( , and econometrics always beats me, to secure my self i would be the regular visitor on wards,
ReplyDeletethanks
Naseema
Pakistan
Trying to play around in Excel and use simulated data to help explain unit roots, differencing, etc. I can easily create 1000 obs of i(1) data with:
ReplyDelete=C4*$C$1+NORM.INV(RAND(),0,1)
where c4 is x and c1 is changed from .75 to 1 (to show a graph of a partially integrated series to a i(1) series). Then showing how differencing makes it stationary.
Question - how would I generate a i(2) or other order series that I could double difference to show this at work to make the second differenced series stationary?
Thanks for this great blog!
Philip Seagraves
Philip: Suppose you've stored the above results in column D. Now just repeat you code using column D instead of column C and store the results in (say) column E.
DeleteDear Professor Dave Giles,
ReplyDeleteFirst of all let me thank you because of your useful blog that is I think the best blog related to econometrics.
Prof I have a question regarding the short-run results in ARDL procedure.
I am running a model in Microfit software by applying ARDL approach. The optimum lag for a five dimension model is (1,2,2,0,2).
My question is that, in the short run for some variable I have two coefficients (because of two lags)with one positive and the other negative sign and both of them are significant, please help me to find out how I have to choose the correct coefficient.
Thanks in advance
Best wishes
I really wish you good health.
Should multicollinearity problem be looked into while doing cointegration?
ReplyDeleteNo - not in my view.
DeleteDear Prof Giles,
ReplyDeleteWhile carrying out Johansen Cointegration Test in E Views there are five assumptions provided. I have two queries. First, how do we decide which assumption has to be accepted while carrying out the test? Second, if all tests show that there is atleast one cointegrating relationship, then what should I infer?
Thanks in advance
If I have nonstationary data in a regression equation and I do not want to difference my series since it will lead to low R2, is it ok to just include a time trend variable? Thanks.
ReplyDeleteIn general, no, definitely not! If all of the variables are I(1) AND they are cointegrated, then you can estimate the model using the levels of the data. Adding a time trend allows for a DETERMINISTIC trend in the data. If the data are integrated, then they have a STOCHASTIC trend. That's a totally different issue.
DeleteHello Prof Giles,
ReplyDeletethanks for the helpful blog! One question concerning the cointegration test. If I conduct a test on cointegration for let's say five non-stationary variables, and cointegration is present, BUT older studies on this topic with the same variables (for another time span) do not find cointegration, what is my conclusion of these conflicting results? Is it possible that time series are cointegrated or not depending on the time span under study?
Thanks!
Yes, that's one possible reason. Another may be the presence of structural breaks, which will confound the cointegration testing,
DeleteDear Professor Giles,
ReplyDeleteWhat a great blog this is, it is very helpfull! I have a few questions related to this subject and hopefully you can help.
I investigate the forecast performance of financial analysts. I have the time series of 400 companies of the MSCI world index and the average forecast of all the analysts for each company, of course also time series. Since I deal with stock price time series and prediction of them it is not a surprise that they are non-stationary.
From cointegration tests I conclude that both series (as expected, for almost all the companies/predictions) are cointegrated.
Now my question is that what does this mean for the R-square if I do an regression of the analysts forecasts on the actual stock prices with OLS? Is it useless? Is it better to do a FM-OLS?
Again thanks for this great blog!
As long as the series are cointegrated, you DON'T have a "spurious regression" problem, and you can interpret the R-squared in the usual way.
DeleteIs this really true? The R2 is after all the 'explained' part of the variance of the 'left-hand-side variable’ (in this case the stock price). But, if the time series are nonstationary, then the variance changes over time?!
DeleteYou probably mean you can use the R2 of the (panel) error correction model?
Let’s take the research from above as an example. If you compare the forecasts of analysts for companies from the American region and compare these with forecasts for the European region, can you compare both R2 and make conclusions? If so why?
I probably misunderstand the value of not having a ‘spurious’ regression, but I really like to understand it.
R2 relates to the sample variance. It;s just a sample statistic.Non-stationarity relates to the population process that generates the data.
DeleteHi Dave,
ReplyDeleteHow about coefficient of error correction term that does not fall between 0 and -1, what does that imply?
If you mean more negative than -1, then the short-run dynamics are "over-compensating". Realistic?
DeleteProfessor Giles,
ReplyDeleteThank you for all of your helpful tutorials. In your second regression of consumption on DPI (with the lags) you state "the long-run mpc works out to be 0.884." Please pardon me if this question is naïve, but how do you determine that? It is obvious in the first regression that it is simply the slope of the relationship between the two. I notice in some earlier responses that you planned to talk more about the distinction between short-run and long-run, perhaps you can just point me to another post.
In the long run C(t) = C(t-1), Y(t) = Y(t-1), etc.
DeleteGather up terms and take the derivative, then the LRMPC is:
(0.356420 - 0.240204) / (1 - (0.984155 - 0.115619)) = (0.11438 / 0.131464 ) = 0.870
I have corrected the number in the post.
Hi
ReplyDeleteCan I use VECM if I have differenced with order 3? As in I(3)?
If you're using economic data it won't be I(3).
DeleteHi Prof,
ReplyDeleteI must estimate an ECM with one dependent and two independent variables. There is a cointegrating relationship between those three but we do not know where it lies. How do you determine the number of lags used on both the dependent and independent (both of them) variables in an error correction model?
Use SIC or AIC, and make sure that you enough lags for the errors to be serially independent.
DeleteThank you for the swift reply. Which of the two information criteria is preferential? I have a case where increasing lags on certain variables improves the AIC but decreases the SIC. Lastly, in terms of the whole process, is determining the number of lags essentially a case of trial and error, wherein we must stumble across the ECM with the best AIC/SIC? Apologies for all the questions, I've found myself quite stuck!
DeleteMany thanks,
Basty Tonks
I prefer SIC - see my other posts on Information Criteria. Remember that you're trying to minimize it's value across competing models. You need to do a broad search.
DeleteGood day Prof. Giles
DeleteThanks for a very informative and helpful post. I always find myself referring to your blog first before looking else where as your posts have helped me resolve a number of issues in the past.
My question builds on what has been discussed here, as well as your comments earlier about dealing with auto-correlation if concerned about the long-run (and not just co-integration).
I too have this 'problem' of my AIC and SIC moving in opposite directions as I try to determine optimal lag length on the VECM. Given your comments and my readings on the topic your advise on preferring SIC makes sense.
I would like to confirm that the process of lag length selection would take place after correcting for the auto-correlation in the residuals?
That is, after running the VECM at the first lag length I pause to check the residuals characteristics and find auto-correlation. Adding more lags helps a little but some AC still obvious (even using the LM test over the Portmanteau Test), but I start to worry about the d.f. issues of having too many lags (and a number of lags which don't make economic sense).
I imagine that once I note this AC issue, I should then bring the Residual Term into the VECM and restart my lag length selection, but I would like to confirm this with you.
Any resources/extra advice you could link me on this matter of lag length and auto-correlation in the VECM would be most appreciated.
Kind Regards
Kerry
Kerry - my apologies for being so slow in responding. The use of AIC/SIC for lag length selection should take place after you have dealt with any autocorrelation in the residuals. The reason is this - the AIC and SIC are based on the log-likelihood function, which in turn assumes independence of the observations. This assumption is violated if you have autocorrelation. I don't have a general resource to refer you to. Sorry!
Deletewhat if the intercept (constant coefficient) is negative? then what to do? what will be the explanation?
DeleteIt doesn't matter what sign it is.
DeleteRespected Sir,
ReplyDeleteI have 3 time series.Two of them are stationary at level and third one is stationary at second difference.These3 are not cointegrated at level but cointegrated at first difference.I am trying to model their relationship.Should I go for VAR or VECM or ARDL? While modelling should I use data at level or at difference?
Regards,
Rohit
It's not possible for them to be cointegrated.
DeleteYou can't use an ARDL mode, if any series is I(2).
Logically, you could estimate a VAR with the levels of the first 2 variables and the second difference of the third variable. I'm not saying that the results will make any economic sense, though.
can you please tell me about the step by step process of johanson co integration and its basic requirements?
ReplyDeletethats is great blog i love this
ReplyDeleteDear Prof. Dave
ReplyDeleteI am facing a peculiar problem. All my tests for cointegration between non stationary time series are suggesting the presence of cointegration, but my error correction term is turning out to be either positive or insignificant or an absolute value of more than 1. How should I interpret this result?
This could be happening for a number of reasons.
DeleteKeep in mind that unit root tests typically have pretty low power, so depending on the tests you're using, you may be getting a "false positive" that one or more of your series are I(1).
Structural breaks tend to lead unit root tests to "discover" unit roots that aren't there, so once again, it may be the case that not all of your series are really I(1).
If you are using seasonally unadjusted quarterly or monthly data, the unit roots that you are detecting at the zero frequency may only be part of the story. There may also be unit roots at the seasonal frequencies - these can be detected using the HEGY tests. This will mess up your cointegration testing.
In short, there could be lots of reasons why your unit root/cointegration tests may be giving false signals. There may not be cointegration at all.
In addition, if you're using the Johansen methodology to test for cointegration, you need to be sure that the VAR model that is used as the basis for this testing is properly specified with respect to lag lengths, serial independence of the errors, and normality of the errors.
Prof. Giles!
ReplyDeleteThank you for an informative post!
I would like to forecast consumption using disposable income as an exogenous variable in R. I have found a cointegrated relationship between the two variables and have estimated an Error Correction Model. However I have difficulties to find a function that produces forecasts for ECM. I've heard that you must create your own function in order to do this forecast, but this is a little bit to hard for me since Im relatively new to R. Do you have any suggestions on how I can create this function, or does it exist a function in R that will produce these forecasts?
Whichever package you're using it's very straightforward. I've prepared a post for you, here: http://davegiles.blogspot.ca/2016/05/forecasting-from-error-correction-model.html
DeleteThank you very much.
DeleteI appreciate your answer!
Dear profesore Giles,
ReplyDeleteI have seen that you use correlogram of variables to acees their level of integration. However, I was wondering is it necessary to analise the ACF and PACF of variables before enbarking on cointegration tests. Namely, recently I've seen in the literature a statement like "since 1st lag PACF of both variable does not exceed 0,75 presence of cointegration is not tested". I am not sure I understand why it is not tested. Can you please share some insight?
You should test for the order of integration of each series using a formal test (such as ADF or KPSS). If the series are integrated, of the same order, then you should test for cointegration. The ACF and PACF plots just provide informal visual information.
DeleteYou said "Now the residuals are serially independent, and the long-run mpc works out to be 0.870." Is 0.870 a typo? Would not it be 0.356?
ReplyDeleteNo, that would be the short-run m.p.c. To get the long-run mp.c. you need to take into account the lags of the dependent variable, in the usual way. And of course the l.r.m.p.c. exceeds the s.r.m.p.c., because the model is dynamically stable (if you look at the coefficient values).
Delete