Yesterday, one of the students from my introductory grad. econometrics class was asking me for more explanation about the connection between the "degrees of freedom" associated with the OLS regression residuals, and the rank of a certain matrix. I decided to out together a quick handout to do justice to her question, and it occurred to me that this handout might also be of interest to a wider group of student readers.
So, here's what I wrote.
Let's take a look at the reason why there are (n – k) “degrees of freedom” associated with the usual linear regression model,
y = Xβ + ε ; ε ~ N[0 , σ2In] ,
y = Xβ + ε ; ε ~ N[0 , σ2In] ,
where X is a non-random matrix with full column rank, k.
First of all, what does the term, “degrees of freedom” mean? It refers to the number of (logically) independent pieces of information in a sample of data. Note that this is quite different from the ides of statistical independence.
By way of a quick example, suppose that we have a sample four values {4, 2, 6, 8}. There are four separate pieces of information here. There is no particular connection between these values. They are free to take any values, in principle. We could say that there are “four degrees of freedom” associated with this sample of data.
Now, suppose that I tell you that three of the values in the sample are 4, 2, and 6; and I also tell you that the sample average is 5. You can immediately deduce that the fourth value has to 8. There is no other logical possibility.
So, once I tell you that the sample average is 5, I’m effectively introducing a constraint. The value of the unknown fourth sample value is implicitly being determined from the other three values, and the constraint. That is, once the constraint is introduced, there are only three logically independent pieces of information in the sample. That’s to say, there are only three "degrees of freedom", once the sample average is revealed.
Now, let’s return to our regression model. Let’s use the following notation
- The OLS estimator of β is: b = (X'X)-1X'y .
- The residuals vector is: e = (y-Xb) = [I-X(X'X)-1X']y
- The matrix, M = [I-X(X'X)-1X'], is idempotent. That is, M' M = M. So its rank equals its trace.
- This trace is tr.(In) - tr.[X(X'X)-1X'] = n - tr.[(X'X)-1X'X] = n - tr.(Ik) = (n - k).
Now, although there are n independent values in the sample of y data, let’s see why there are only (n – k) logically independent values in the n-element residuals vector, e. When we transform the n elements in y into the n elements in e, we use a transformation matrix that has less than full rank. The M matrix is (n x n), but its rank is only (n – k).
This reduction in rank has the effect of reducing the number of independent pieces of information by the same amount. That is, of the n elements in e, only (n – k) of them are independent, given the way that they were constructed (using y and M).
Keep in mind what we mean by the “rank” of a matrix. It’s the number of linearly independent rows or columns – whichever is the smaller. Any reduction in rank results in a reduction in the number of logically independent elements that we end up with after the y vector is transformed into the e vector.
Let’s take a simple numerical example to illustrate what’s happening here. Let n = 3 and k = 2, and suppose that the first column of the regressor matrix, X, is a column of "ones" for the intercept, while the second column takes the values 0, 1, and 0.

Notice that although M has 3 rows and columns, its rank is only 1. (That is, its rank is n – k.) Specifically, the row of zeroes reduces the rank from 3 to 2; and then we see that the first row is just the negative of the third row, and this reduces the rank from 2 to 1.
In other words, once I tell you the value of e1, I’ve actually told you the entire e-vector! There is only one “independent” element in e. Or, as we say, there is only one "degree of freedom".
You can check for yourself that if we go through the same exercise, but with the second column of X taking the values 1, 2, and 3, then we end up with
In this matrix, row 1 equals row 3; and row 2 is the negative of twice row 1. Each of these two relationships reduces the rank of M, its rank is again 1.
Again, once I tell you the value of e1, I’ve actually told you the entire e-vector! There is only one “independent” element in e. Or, as we say, there is only one "degree of freedom".
I hope this is helpful!
© 2012, David E. Giles

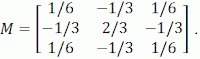

Fantastic post, though there is a math error in the second bullet where you have e=y-Xb=M (essentially) when it should be My.
ReplyDeleteAs a follow up, when considering the AIC it asks for the number of parameters. Is this always the same as the k you use when thinking about degrees of freedom?
I'm not sure I can think of a simple example... Consider m principal components, E, from X (which is TXn) to create F=XE. Suppose you regress X=FB+e=XEB+e. EB will be mXn, but presumably only has m+n free parameters since they can be used to reconstruct EB. If B=E', then there are only m parameters. Does this make sense?
I slightly messed up that example, E would be nXm, B would be mXn. So the number of parameters in the first case would be n^2, 2nm in the second case, and nm in the third.
ReplyDeleteJohn - thanks for both comments. Omission fixed - thank you!
DeleteSecond - it will be the number of "free" parameters. Consider restricted least squares, where there are "n" observations, "k" regressors, and "J" independent linear restrictions on the coefficients. Then the d.o.f. are (n-k+J), and (k-J) would be the appropriate quantity to use when constructing AIC, BIC, etc.
When you say "n-k+J" d.f. is used in calculation of AIC, what do you mean by k exacly?
DeleteThat is to say, say,
Y ~ constant + B2*U + B3*V + B4*W then k=3 or k=4? Is the constant (intersection) thought as a regressor? In some books, it says so.
Absolutely - the "constant term" is a vector of "ones", with a coefficient. That coefficient is just like the other regression coefficients - you count it. So k=4. This is the universal convention - not just in some books.
DeleteBrilliant explanation! I think most of the econometrics professors don't know how to explain that. Thank you.
ReplyDeleteThanks for the very kind comment.
DeleteProfessor,
ReplyDeleteHow simply you have explained that as constraints to the system increase the number of independent information (degrees of freedom) come down, which is further reduced by the reduction in rank in the case of the matrix.
This raises the doubt that when data is structured for proving a hypothesis, we are ignorant of the fact that actually less are independent sets of information as constraints tend to increase. Thus when the hypothesis is tested with more number of constraints, we have a diminishing nature of independence in the information sets.
Procyon Mukherjee
Procyon - thank you.
DeleteVery good.
ReplyDeleteExcellent explanation!
ReplyDeleteThank you!
ReplyDeleteDG
Thank you very much.
ReplyDeleteErdogan CEVHER
Well said in understandable words. Thank you.
ReplyDeletethank you sir.
ReplyDelete