What test do you usually use if you want to test if the errors of your regression model are normally distributed? I bet it's the Jarque-Bera (1982, 1987) test. After all, it's a standard feature in pretty well every econometrics package. And with very good reason.
However, there some things relating to this test that you may not have learned in your econometrics courses. Let's take a look at them.
What's the Motivation for the Test?
The basic idea behind the J-B test is that the normal distribution (with any mean or variance) has a skewness coefficient of zero, and a kurtosis coefficient of three. (That is, it has zero "excess kurtosis".) So, if we can test if these two conditions hold, against a suitable (family of) alternative(s), then we're in business.
The trick is to formulate a test whose associated statistic has a known distribution, if H0 (normality) is true; and which has decent power properties. If this can't be done easily for finite samples, then at least we may be able to do this for the case where the sample size is very, very large.
Notice that the null hypothesis involves imposing two restrictions. So, you might guess that if we can construct a LR, Wald, or LM test, with normality "nested" within a more general family of distributions, then asymptotically the test statistic will be χ2 distributed with 2 degrees of freedom, if H0 is true.
The usual formulation of the J-B test statistic when we test for normality of the errors in an OLS regression model is:
JB = n [(√b1)2 / 6 + (b2 - 3)2 / 24] , (1)
where n is the sample size, and √b1 and b2 are the sample skewness and kurtosis coefficients. More specifically, if the OLS residuals are ei (i = 1, 2, ..., n), and mj = n-1∑(eij) ; j = 1, 2, 3, 4 are their first four sample moments, then √b1 = [(m3) / (m2)3/2], and b2 = [m4 / (m2)2].
A sufficiently large value of JB will lead us to reject the hypothesis that the errors are normally distributed. We'll come back to the formula for JB below.
How is it Related to Earlier Work?
Carlos Jarque and Anil Bera were both grad. students in econometrics at the Australian National University when they developed their test. (Not bad!) As they were well aware, the same idea had been put forward by Bowman and Shenton (1975). However, the latter authors simply showed that the asymptotic null distribution of JB is χ2 with 2 degrees of freedom. They didn't explore the power properties of the test, or its behaviour in finite samples.
Jarque and Bera went further - they derived the JB statistic as the LM test statistic for a major class of problems. This has some important implications.
Jarque and Bera went further - they derived the JB statistic as the LM test statistic for a major class of problems. This has some important implications.
Is the J-B Test Optimal?
Yes, you can say that the J-B test is optimal - in the following sense. The J-B test is the LM test for the nested null hypothesis of normality against the maintained hypothesis that the data are generated by Pearson family of distributions. Being an LM test, it has maximum local asymptotic power, against alternatives in the Pearson family. (So does the LR test, but the LM test is much simpler to compute for this testing problem.) In fact, Jarque and Bera (1987) also showed that the J-B test has excellent asymptotic power against alternatives outside that family of distributions.
How Well Does the J-B Test Perform in Finite Samples?
As with any LM test, the J-B test has asymptotic validity. However, if it is applied in small samples (using a critical value associated with its asymptotic χ2(2) distribution), then there can be considerable "size distortion". That is, the actual probability of rejecting H0 when it is true can be very different from the assumed significance level, based on the asymptotic distribution.
This issue, and the associated implications for the power of the J-B test were also investigated by Jarque and Bera (1987) in a Monte Carlo experiment. They found that the J-B test performed at least as well as other competitor tests, even for quite small sample sizes. In addition, they found that that the power of the test depends in part on the form of the "hat matrix" (i.e., the matrix X(X'X)-1X') associated with the regressors in the model.
However, more recent evidence suggests that the power of the J-B test can be quite low in small samples, for a number of important alternative hypotheses - e.g., see Thadewald and Buning (2004).
I'll address this aspect of the J-B test more fully in a later post.
What if the Regression Doesn't Include an Intercept?
This last question deals with something that is almost always overlooked in classroom discussions of the J-B test. If you haven't actually read the original J-B work (in particular, Jarque and Bera, 1987) then you probably aren't aware that the formula for the test statistic is actually somewhat more complicated than that given in equation (1) above.
The full formula is:
JB = n [(√b1)2 / 6 + (b2 - 3)2 / 24] + n[3m12 / (2m2) - m3m1 / m22] . (2)
However, if the regression model includes an intercept then the OLS residuals will sum to zero, and m1 = 0. So, in this case the expression in (2) collapses to that in (1). If you fit your regression through the origin, then formula (2) is what should be used to compute the J-B test statistic.
(You see, you can actually learn something useful by reading the original sources, rather than relying on what your text book says!)
(You see, you can actually learn something useful by reading the original sources, rather than relying on what your text book says!)
Now, how much of a difference might this make? Here's just one empirical example. I've performed a small Monte Carlo experiment with the following design:
(a) The data-generating process (DGP) is
yi = β0 + β1xi + εi ; εi ~ i.i.d. N[0 , σ2]
The same model is estimated by OLS, with n = 5,000 observations, and the J-B test statistic is computed using the usual formula, as in equation (1).
(b) The DGP is
yi = β1xi + εi ; εi ~ i.i.d. N[0 , σ2] .
The same model is estimated by OLS with n = 5,000 observations, and the J-B test statistic is (incorrectly) computed using the usual formula, as in equation (1).
(It's easily shown that the results given below are invariant to the parameter values used in the DGP's.)
(a) The data-generating process (DGP) is
yi = β0 + β1xi + εi ; εi ~ i.i.d. N[0 , σ2]
The same model is estimated by OLS, with n = 5,000 observations, and the J-B test statistic is computed using the usual formula, as in equation (1).
(b) The DGP is
yi = β1xi + εi ; εi ~ i.i.d. N[0 , σ2] .
The same model is estimated by OLS with n = 5,000 observations, and the J-B test statistic is (incorrectly) computed using the usual formula, as in equation (1).
(It's easily shown that the results given below are invariant to the parameter values used in the DGP's.)
Each part of the experiment is replicated 20,000 times.The proportion of times that the J-B statistic exceeds the χ2(2) critical values, for assumed significance levels of 1%, 5%, and 10% are recorded. As the errors are normally distributed in the DGP's, H0 is true, so these observed empirical rejection rates are the true significance levels.
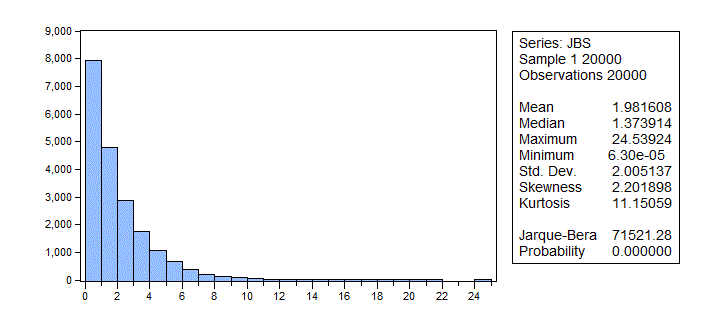
For part (a) of the experiment, the empirical distribution of the 20,000 J-B values looks like this:
The mean and variance of a χ2 distribution equal the degrees of freedom (2 in our case), and twice the degrees of freedom, respectively. So, n = 5,000 seems to approximate the asymptotic case pretty well. Also, for this case, the empirical rejection rates are 1.0%, 4.7%, and 9.8%. These match the assumed values very well indeed.
The mean and standard deviation of this empirical distribution now exceed two in value, and the empirical rejection rates associated with the test are approximately 2.1%, 7.7%, and 14.0%.
There's a noticeable upward size distortion associated with the test. This is because the J-B statistic has been computed (wrongly) using the formula in (1), rather than using the correct formula in (2). So, be careful not to use the usual formula for the J-B test if your regression model is fitted through then origin.
The EViews program and workfile that I used are on the code page for this blog. You can easily modify the program if you want to investigate the small-sample size-distortion and power of the (properly applied) J-B test for yourself.
References
Bera, A. K. amd C. M. Jarque, 1982. Model specification tests: A simultaneous approach. Journal of Econometrics, 20, 59-82.
Bowman, K. O. and L. R. Shenton, 1975. Omnibus contours for normality based on √b1 and b2. Biometrika, 62, 243-250.
Jarque, C. M. and A. K. Bera, 1987. A test for normality of observations and regression residuals. International Statistical Review, 55, 163-172.
Thadewald, T, and H. Buning, 2004. Jarque-Bera test and its competitors for testing normality - A power comparison. Discussion Paper Economics 2004/9, School of Business and Economics, Free University of Berlin.

No comments:
Post a Comment
Note: Only a member of this blog may post a comment.