This post is one of a sequence of posts, the earlier members of which can be found here, here, here, and here. These posts are based on Giles (2014).
Some of the standard tests that we perform in econometrics can be affected by the level of aggregation of the data. Here, I'm concerned only with time-series data, and with temporal aggregation. I'm going to show you some preliminary results from work that I have in progress with Ryan Godwin. Although these results relate to just one test, our work covers a range of testing problems.
I'm not supplying the EViews program code that was used to obtain the results below - at least, not for now. That's because what I'm reporting is based on work in progress. Sorry!
Some of the standard tests that we perform in econometrics can be affected by the level of aggregation of the data. Here, I'm concerned only with time-series data, and with temporal aggregation. I'm going to show you some preliminary results from work that I have in progress with Ryan Godwin. Although these results relate to just one test, our work covers a range of testing problems.
I'm not supplying the EViews program code that was used to obtain the results below - at least, not for now. That's because what I'm reporting is based on work in progress. Sorry!
As in the earlier posts, let's suppose that the aggregation is over "m" high-frequency periods. A lower case symbol will represent a high-frequency observation on a variable of interest; and an upper-case symbol will denote the aggregated series.
So,
So,
Yt = yt + yt - 1 + ......+ yt - m + 1 .
If we're aggregating monthly (flow) data to quarterly data, then m = 3. In the case of aggregation from quarterly to annual data, m = 4, etc.
Now, let's investigate how such aggregation affects the performance of the well-known Jarque-Bera (1987) (J-B) test for the normality of the errors in a regression model. I've discussed some of the limitations of this test in an earlier post, and you might find it helpful to look at that post (and this one) at this point. However, the J-B test is very widely used by econometricians, and it warrants some further consideration.
Consider the following small Monte Carlo experiment.
To begin with, the data-generating process (DGP) is of the form:
yt = β0 + β1 xt + ut ; ut ~ N[0 , 1] ; where xt = 0.1t + N[0 , 1] .
The model that is estimated, however, uses aggregated data:
Yt = β0 + β1Xt + vt .
We've looked at two aggregation levels - m = 3, and m = 12, but only results for m = 3 are discussed below.
Using 20,000 replications, the Monte Carlo experiment looks first at the distortion in the size (significance level) of the J-B test, in the face of this type of aggregation.
The null hypothesis is that the errors are normally distributed, while the alternative hypothesis is that they are non-normal. Various sample sizes are considered, ranging from T = 12 to T = 5,000. As you can see from the DGP above, to begin with the null hypothesis is true.
In the following tables, α* is the "nominal" size of the test. It's the significance level that we think we're using. That is, we pick a significance level (α*) and then, based on the asymptotic null distribution of the J-B test statistic (which is χ2(2)), we have a critical value, c(α*).
In the experiment, the actual size of the test will be the number of times that the J-B statistic exceeds c(α*), expressed as a proportion of 20,000, when the null is true. We call the difference between the actual and nominal sizes of the test the "size distortion".
In our case, if T is small, there will be some distortion coming from the use of a critical value that is valid only when T is infinitely large. There will also be some size distortion coming from the aggregation of the data, and this may be present even if T is extremely large. Let's find out if this is the case.
In the table above, we consider three typical values for the nominal significance level. The numbers in blue are for the case where there is no temporal aggregation. The figures in red are for case of temporal aggregation with m = 3. (Recall, this is like aggregating monthly flow data into quarterly data.)
Looking at the blue numbers we see that there is considerable size distortion when T is relatively small, as a result of using critical values based on the asymptotic χ2 distribution for the J-B statistic. Of course, this is what we typically do in practice. The direction of the size distortion depends on the choice of α*. Quite large sample sizes are needed to fully eliminate this distortion. Similar results have been reported by various authors (e.g., see here).
Looking at the red numbers in the above table, we see the combined effect of the small sample distortion, and the aggregation distortion. The latter effect has an increasing impact as T grows, at least for the range of sample sizes considered here. Why is this? A close inspection of the empirical sampling distributions for the J-B statistic in the experiment reveals that their means and variances are converging to the values 3 and 10 (instead of 2 and 4, as expected for the χ2(2) distribution), as T grows.
Looking at the red numbers in the above table, we see the combined effect of the small sample distortion, and the aggregation distortion. The latter effect has an increasing impact as T grows, at least for the range of sample sizes considered here. Why is this? A close inspection of the empirical sampling distributions for the J-B statistic in the experiment reveals that their means and variances are converging to the values 3 and 10 (instead of 2 and 4, as expected for the χ2(2) distribution), as T grows.
Now let's investigate the power of the J-B test. To do this we need to consider the rate at which the null hypothesis, that the regression errors are normal, is rejected when that hypothesis is false. This means that we need to change the DGP. By way of illustration, let's have Student-t errors:
(Choosing the degrees of freedom for the Student-t distribution ensures that the errors have a finite variance.)
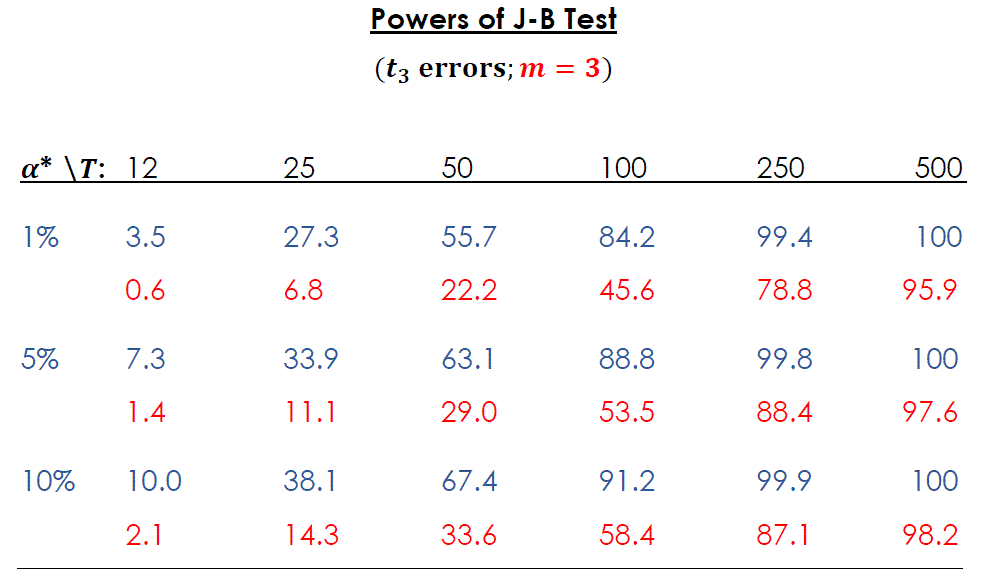
Here are some illustrative results for the power of the J-B test:
Once again, the numbers in blue are for the case where there is no temporal aggregation. The figures in red are for case of temporal aggregation with m = 3. All of these values are implicitly associated with one point on the corresponding power curve, as we're considering just one "degree of falseness" for the null hypothesis.
As expected, all of the powers increase with increasing T - the J-B test is "consistent". Comparing the red and blue numbers we also see that temporal aggregation reduces the power of the test, for any finite sample size. This reduction can rather substantial. As far as I know, this isn't a result you'll find anywhere in the literature.
Moreover, when T = 12 and the data are temporally aggregated, the power of the J-B test is lower than the (nominal) significance level. The test has the unfortunate property of being "biased". The probability of (correctly) rejecting the null hypothesis when it's false is less than the probability of (wrongly) rejecting the null hypothesis when it's true! Actually it's known that this can happen for the J-B test against certain alternative hypotheses, even when there's no aggregation effect. Again, see here.
The take-away message?
It's always a good idea to know how robust our tests are to departures from the assumptions on which they're based. It's well known that the J-B test, and other such "omnibus tests" are far from perfect when used with samples of modest size. If, in addition, you're working with temporally aggregated time-series data, then you have even more reason to proceed with caution.
References
Giles, D. E., 2014. The econometrics of temporal aggregation: 1956 - 2014. The A. W. H. Phillips Memorial Lecture, New Zealand Association of Economists Annual Meeting, Auckland, July.

No comments:
Post a Comment
Note: Only a member of this blog may post a comment.