Estimating Elasticities, All Over Again

I had some interesting email from Andrew a while back to do with computing elasticities from log-log regression models, and some related issues.

In his first email, Andrew commented:

"I am interested in the elasticity of H with respect to W, e.g., hours with respect to wages. For simplicity, assume that W is randomly assigned, and that the elasticity is identical for everyone.

Standard practice would be to regress log(H) on a constant and log(W). The coefficient on log(W) then seems to be the elasticity, as it estimates d log(H) / d log(W).

But changes in log( ) are only equal to changes in percent in the limit as the changes go to zero. In practice, one typically uses discrete data. Because the changes in W may be large, the resulting coefficient is just a first order approximation of the elasticity, and is not identical to the true elasticity."

Let's focus on the third paragraph. Keep in mind that log( ), here, refers to "natural" (base 'e') logarithms.

Andrew is quite correct, and this is something that we often overlook when teaching econometrics, or when interpreting someone's regression results. I sometimes refer students to this useful piece by Kenneth Benoit. Here's a key extract from p.4:

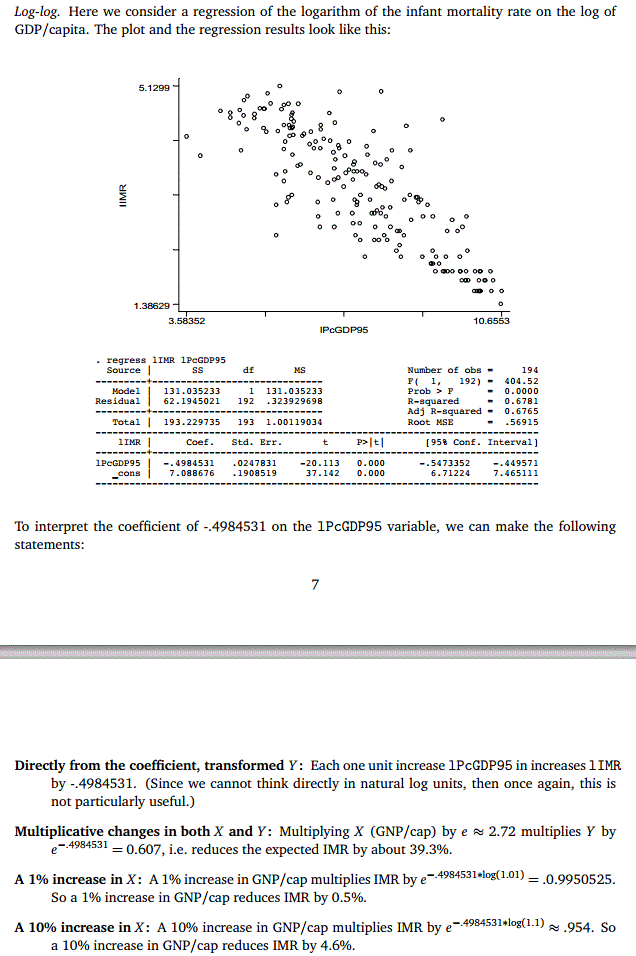
Kenneth then provides a useful example (pp. 7-8):

What would we conclude if we just looked at the estimated coefficient of -0.4984531, and took this to be "the" estimated point elasticity? Well, we'd then say that:

• A 1% increase in GNP/cap would lead to a decrease of 0.498% in IMR. O.K., so far.
• A 10% increase in GNP/cap would lead to a decrease of 4.98% in IMR. Not so good!
• A 20% increase in GNP/cap would lead to a decrease of 9.96% in IMR.

How inaccurate is this last result? 

If we perform the calculation correctly, the answer is 100*{1 - exp[-0.4984531*log(1.2)]} = 8.7%. That's quite different from 9.96%! 

And if we looked at the effect of a 40% increase in GNP/cap, the correct expression for the implied decrease in IMR is 18.3%. Not (50*0.4984531) = 24.92% !

The bigger the (%) change in the regressor, the less accurate is the estimated coefficient itself as a measure of the point elasticity.

As it turns out, Andrew was actually thinking of a somewhat more subtle point, as he explained in a subsequent email:

"The issue I am thinking about, though, is whether it is appropriate to think of the coefficient in a log-log regression as actually being an elasticity. Given that the data used to estimate the model are discrete, it seems the model is mis-specified.......

In other words, using the numbers from your example, if the data show a 20% increase in GNP/cap and a decrease in IMR of 8.7%, I don't think the log-log regression would recover the correct elasticity. The reason is that logs are only approximations of percent changes, and with such large movements these approximations would likely exhibit noticeable error. However, this is all just my intuition. I haven't sat down and run the simulations, or done the calculations. I was just wondering if you knew of literature that addressed this issue. It seems likely we could determine whether the bias pushes up or down, I'm just not sure which is correct."

I think that Andrew is correct, but I can't point to any supporting literature, off-hand.

Of course, the use of a log-log regression model in the first place can be subjected to more basic criticism. By construction, it imposes a constant elasticity, regardless of the values of the regressor and the dependent variable (at least for small changes in the former, ☺).

Often, this restriction is inappropriate. In contrast, and as every first-year undergraduate student of economics knows, a purely linear model allows the elasticity to vary continuously as the values of the variables change. For this reason, when reporting an elasticity based on a linear-in-variables regression model we typically report just a "representative" value, such as e = b(x* / y*), where b is the OLS estimate of the regression coefficient, and x* and y* are the sample means of the regressor and the dependent variable.

All of the discussion so far has related to what we usually call "point elasticities".

Again, as we learn in our introductory "Principles" class, we could also consider "arc elasticities". However, in the way that these are usually defined, they are not unique. An interesting alternative is discussed by Andres Vasques (1995). He proposes an arc elasticity that is defined in terms of the logarithmically transformed data, and show that it has some interesting, and intuitively appealing properties. For example, it equals the point elasticity at some point over which the arc is taken.

It's worth keeping in mind that there's more than on way to estimate an elasticity.

© 2015, David E. Giles