Back in 2013 I wrote a post that was titled, "Forecasting From Log-Linear Regressions". The basis for that post was the well-known result that if you estimate a linear regression model with the (natural) logarithm of y as the dependent variable, but you're actually interested in forecasting y itself, you don't just report the exponentials of the original forecasts. You need to add an adjustment that takes account of the connection between a Normal random variable and a log-Normal random variable, and the relationship between their means.
Today, I received a query from a blog-reader who asked how the results in that post would change if the dependent variable was the square root of y, but we wanted to forecast the y itself. I'm not sure why this particular transformation was of interest, but let's take a look at the question.
In this case we can exploit the relationship between a (standard) Normal distribution and a Chi-Square distribution in order to answer the question.
I'm going to "borrow" heavily from my earlier post.
Suppose that we're working with a regression model of the form
Suppose that we're working with a regression model of the form
√(yt) = β1 + β2x2t + β3x3t + ......+ βkxkt + εt ; t = 1, 2, ...., n.
The explanatory variables are assumed to be non-random, so that rules out models with lagged values of the dependent variable appearing as regressors. Let's also assume that the errors have a zero mean, and are serially independent,and homoskedastic (with a variance of σ2). Crucially, we'll also assume that they are Normally distributed.
Once we estimate the model, we have the "fitted" values for the dependent variable. That is, we have values of [√(yt)]* = b1 + b2x2t + ..... + bkxkt, where bi is the estimated value of βi (i = 1, 2, ......, k). These estimates might be obtained by OLS, but that's not crucial to the following argument.
Now, we're likely to be more interested in fitted values expressed in terms of the original data - that is, in terms of y itself, rather than √(y) .
You might think that all we have to do is to apply the inverse of the square root transformation, and the fitted values of interest will be yt* = {[√(yt)]*}2. Unfortunately, just squaring the original forecasts will result in an unnecessary distortion.
Let's see why.
If εt is Normally distributed, then √(yt) is also Normally distributed, with a mean of (β1 + β2x2t + β3x3t + ......+ βkxkt), and a variance of σ2. Another way of describing √(yt) is that it is σZ + (β1 + β2x2t + β3x3t + ......+ βkxkt), where Z is a Standard Normal variate.
Now consider yt itself. We get this by squaring the√(yt) random variable, so we can write:
yt = σ2Z2 + (β1 + β2x2t + β3x3t + ......+ βkxkt)2 + 2σZ(β1 + β2x2t + β3x3t + ......+ βkxkt).
Taking expectations,
E[yt] = σ2 E[Z2] + (β1 + β2x2t + β3x3t + ......+ βkxkt)2,
because the mean of Z is zero.
Recalling that Z2 is a Chi-Square variate with one degree of freedom, and that the mean of a Chi-Square variate equals its degrees of freedom, we immediately see that
E[yt] = (β1 + β2x2t + β3x3t + ......+ βkxkt)2 + σ2.
So, if we want to obtain forecasts for y, we should square the forecasts of √(y), but then we need to add σ2.
Of course, σ2 is unobservable but we can replace it with its unbiased estimator, s2. The latter is the sum of squared residuals (from the original regression, with √(yt) as the dependent variable), divided by the degrees of freedom, (n - k). In fact, it can be shown that adding this adjustment term is exactly equivalent to using Duan's (1983) "smearing estimate" for our re-transformation of the dependent variable
Failure to add this extra term will result in point forecasts that are distorted in a downwards direction. Of course, the magnitude of this distortion will depend on both the scale of measurement for our y data, and the signal-to-noise ratio in our regression model.
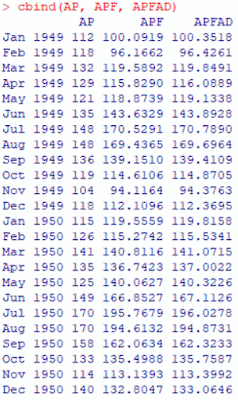
The time series "APF" is the series of naive within-sample predictions, obtained by simply squaring the fitted values for √(AP). The time-series "APFAD" incorporates the adjustment term discussed above. In this particular case, s = 0.5098, so there's not a huge difference between APF and APFAD:
etc.
However, the sum of the squared (within-sample) prediction errors, based on AP and APF is 42318.42, while that based on AP and APFAD is 42310.45. So, there's a bit of improvement in overall forecast performance when we take the adjustment term into account.
A final comment is in order. Although we've been able to see how to "back out" appropriate forecasts of y when the original regression has a dependent variable that is either log(y) or √(y). We were able to do this only because when the inverses of these particular transformations are applied to a Normal random variable, the resulting new random variable has a known distribution. This little "trick" is not going to work - at least, not easily - for arbitrary non-linear transformations of y.
Cowperwait, P. S. P. and A. V. Metcalf, 2009. Introductory Time Series With R. Springer, Dordrecht.
Duan, N., 1983. Smearing estimate: A nonparametric retransformation method. Journal of the American Statistical Association, 78, 605-610.

I really can't overstate this - thank you so, so much. This is an enormous help, and I really appreciate it.
ReplyDeleteYou're most welcome - it was an interesting question.
DeleteAnd just to explain - I've been playing around with replication experiment for a paper update. In order to conform to the previous procedure I've set up a Box-Cox transformation, but unlike the original paper, I'm working with a square root instead of a log on my dependent variable.
ReplyDeleteActually, I had been working through the old Teekens and Koerts paper to understand the back-transformation process, but I got pretty stuck when my results were somehow different than the paper I was replicating. I stumbled across your blog only to find out that I wasn't crazy - it seems like the authors misapplied the results to their model. So that's twice now you've been a huge help!
Happy to have been able to help a little. :-)
DeleteCorrect me if I'm wrong, but if rather than manually transforming your response and using lm and predict.lm you instead fit a glm with family = gaussian(link = "log") and then predict with predict.glm, then all of this is taken care of you. Right?
ReplyDeleteNo, I don't think so - the transformation is square root, not log.
DeleteSorry, I meant gaussian(link = "sqrt"). I was thinking about your earlier post about log-linear regression when I wrote "log".
ReplyDeleteO.K. - in R, you're right. Of course, my main point still holds. And practitioners who're not using R meed to know what to do. Thanks for the helpful comment.
Delete